![\begin{picture}
(62.5,35)(-2.5,-2.5)
\color [rgb]{0,0.6,0}
\multiput(20,0)(...
...0){\circle*{1}}
\put(10,20){\circle*{1}}
\put(10,30){\circle*{1}}\end{picture}](img1203.gif)
Definition: Sei G=(V,E) ein ungerichteter, schlichter Graph. Ein Matching M in G ist eine Teilmenge von E, so daß keine zwei Kanten aus M einen Endpunkt gemeinsam haben.
![\begin{picture}
(62.5,35)(-2.5,-2.5)
\color [rgb]{0,0.6,0}
\multiput(20,0)(...
...0){\circle*{1}}
\put(10,20){\circle*{1}}
\put(10,30){\circle*{1}}\end{picture}](img1203.gif)
Definition:
- 1.
- Ein Matching M in G=(V,E) heißt perfekt (oder vollkommen), falls
- 2.
- Ein Matching M heißt ,,Matching maximaler Kardinalität`` (engl. maximum matching) in G, falls es in G kein Matching M' mit |M'|>|M| gibt. (
durchgehend geringelt (rot) im Beispiel)
- 3.
- Ein Matching M heißt maximal in G, falls es bezüglich ,,
`` maximal ist. (engl. maximal matching,
gepunktet geringelt (grün) im Beispiel)
Definition:
- 1.
- Ein einfacher Pfad (Kreis)
heißt alternierend bzgl. eines Matchings M, falls die Kanten
, abwechselnd in M und nicht in M liegen.
![\begin{picture}
(95,35)
\color [rgb]{0,0.6,0}
\multiput(40,10)(-2.5,0){4}{\...
...\makebox(5,5)[b]{$v_1$}}
\put(0,0){\makebox(95,5){gerade L''ange}}\end{picture}](img1208.gif)
- 2.
- Ein alternierender Pfad heißt augmentierend, falls er bzgl. ,,
`` maximal ist und an beiden Enden ungematchte Kanten hat.
![\begin{picture}
(70,20)
\color [rgb]{0,0.6,0}
\multiput(50,10)(-2.5,0){4}{\...
...4){\line(1,2){2}}
\put(64,18){\vector(0,-1){7}}
\color {black}
\end{picture}](img1209.gif)
Bemerkung: Es kann keine augmentierenden Kreise geben.
Definition: Sei G=(V,E) ein Graph. Wenn V in zwei nichtleere Teilmengen V1 und V2 partitioniert werden kann (,
), so daß
ist, so heißt G bipartit (G=(V1,V2,E)).
![% latex2html id marker 26238
\fbox {\parbox[c]{12.45cm}{\textbf{Heiratssatz:}
(F...
...*} wobei N$(V)$\space die Nachbarschaft von $V$\space (in $V_2$) bezeichnet.
}}](img1213.gif)
![\begin{picture}
(25,25)
\multiput(5,5)(0,5){4}{\circle*{1}}
\multiput(20,5)(0,...
...,4)[t]{$V_2$}}
\put(5,17.5){\oval(5,10)}
\put(20,15){\oval(5,15)}\end{picture}](img1214.gif)
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Ein Graph $G=(V,E)$\space hat ein perf...
... S\vert$
Zusammenhangskomponenten ungerader Gr\uml {o}\ss{}e enth\uml {a}lt.
}}](img1215.gif)
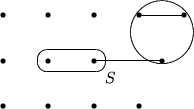
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}(Berge, 1957)\\ Ein Matching hat maxima...
...\uml {a}t genau dann, wenn es keinen
augmentierenden Pfad daf\uml {u}r gibt.
}}](img1217.gif)
Definition: Seien S, T zwei Mengen, dann bezeichneLemma: Sei M ein Matching, P ein augmentierender Pfad bzgl. M. Dann ist auchdie symmetrische Differenz von S und T, d.h.
.
![\begin{picture}
(90,22)(0,2.5)
\color {red}
\multiput(20,20)(-2.5,0){4}{\be...
...makebox(5,5)[l]{$M \ominus P$}}
\put(85,15){\makebox(5,4)[t]{$P$}}\end{picture}](img1223.gif)
![]()
![]()
Verfeinertes Schema:
![]() ;
while
;
while ![]() augmentierender Pfad bzgl. M do
l := Länge des kürzesten augmentierenden Pfades bzgl. M;
bestimme eine bzgl. ,,
augmentierender Pfad bzgl. M do
l := Länge des kürzesten augmentierenden Pfades bzgl. M;
bestimme eine bzgl. ,,![]() `` maximale Menge
`` maximale Menge ![]() augmentierender Pfade bzgl. M, die alle Länge l haben und knotendisjunkt sind;
augmentierender Pfade bzgl. M, die alle Länge l haben und knotendisjunkt sind;
![]() ;
od
;
od
![]()