



Next: Transformation des Definitions- bzw.
Up: Rekursionsgleichungen
Previous: Charakteristisches Polynom
Für lineare und nicht lineare Rekursionsgleichungen erhält man oft eine Lösung, indem man die
fn als Koeffizienten einer Potenzreihe betrachtet und eine geschlossene Form, der dadurch
definierte Funktion sucht.
Definition: Für eine Folge 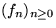 ist die ``erzeugende Funktion``
definiert als:
ist die ``erzeugende Funktion``
definiert als:
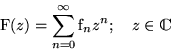
Exponentielle Erzeugendenfunktion:
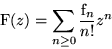
auch Notation:
![\begin{displaymath}
\text{F}(z)=\sum\limits_{n\gt}\text{f}_nz^n \Rightarrow \text{f}_n=[z^n]\text{F}(z)\end{displaymath}](img81.gif)
Sei 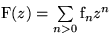 und
und 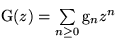
| Erz. Fkt. |
n-tes Folgenglied |
|
Anmerkungen: |
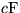 |
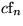 |
|
|
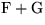 |
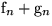 |
|
|
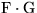 |
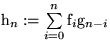 (Konvolution)
(Konvolution) |
|
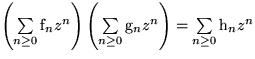 |
| |
|
|
(mit 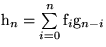 ) ) |
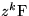 |
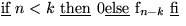 |
|
|
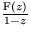 |
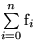 |
|
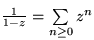 |
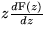 |
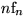 |
|
|
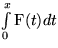 |
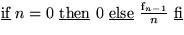 |
|
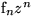 (,,geht über auf``) (,,geht über auf``) 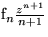 |
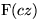 |
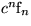 |
|
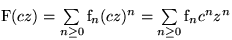 |
Beispiel:
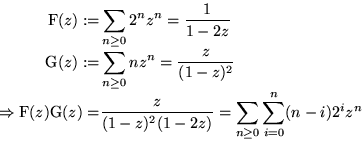
Partialbruchzerlegung:
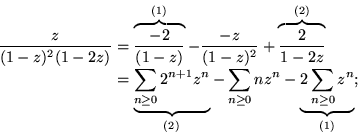
Also:
(z)...
...\geq 0}(2^{n+1}-n-2)z^n\right) \\
&= 2^{n+1}-n-2;\end{split}\end{displaymath}](img108.gif)




Next: Transformation des Definitions- bzw.
Up: Rekursionsgleichungen
Previous: Charakteristisches Polynom
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
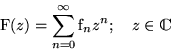
ist die ``erzeugende Funktion`` definiert als:
![]()
![]()
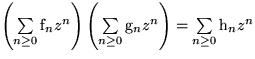
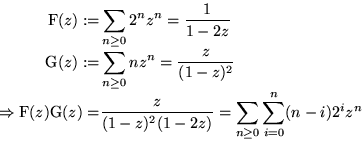
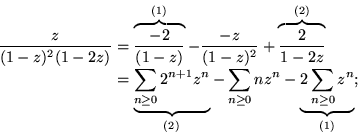
(z)...
...\geq 0}(2^{n+1}-n-2)z^n\right) \\
&= 2^{n+1}-n-2;\end{split}\end{displaymath}](img108.gif)