



Next: Hashing
Up: Binäre Suchbäume
Previous: Natürliche binäre Suchbäume
Definition:
Ein AVL-Baum ![[*]](http://wwwbode.informatik.tu-muenchen.de/icons/latex2html-97.1/gif/foot_motif.gif) ist ein
spezieller binärer Suchbaum, der neben den Sortierungsbedingungen auch
die folgende Höhenbalancierungen erfüllt. Für den Knoten v gilt:
ist ein
spezieller binärer Suchbaum, der neben den Sortierungsbedingungen auch
die folgende Höhenbalancierungen erfüllt. Für den Knoten v gilt:
| Höhe(lUBv) - Höhe(rUBv) | 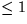
Lemma:
Ein AVL-Baum der Höhe h hat mindestens nh= Fib(h+2) Blätter.
Beweis:
Induktion nach h:
- I)
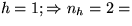 Fib(3);
Fib(3);
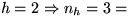 Fib(4);
Fib(4);
- II)
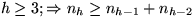
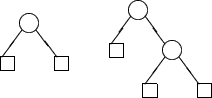
Bei einem bzgl. der Blätterzahl minimalen AVL-Baum der Höhe h darf nur
einer der Unterbäume der Höhe h-1 haben. Der andere muß kürzer sein,
aber wegen der Balancierungsbedingung mindestens Höhe h-2 haben. Beide
sind natürlich minimale AVL-Bäume. Also gilt nh = nh-1+nh-2. Dies
ist genau die Bestimmungsgleichung für Fib(h+1).

Folgerung:
- AVL-Bäume der Höhe h haben mindestens Fib(h+2) Blätter, also Fib(h+2)-1 interne Knoten.
- Da anderseits gilt: Fib(n)
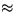
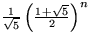 , hat ein AVL-Baum mit n-Blättern
(oder interne Knoten) die Höhe
, hat ein AVL-Baum mit n-Blättern
(oder interne Knoten) die Höhe 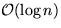 . Dies ist ein bedeutender Fortschritt gegenüber der bisweilen bei natürlichen Suchbäumen
entstehenden Zeitkomplexität von
. Dies ist ein bedeutender Fortschritt gegenüber der bisweilen bei natürlichen Suchbäumen
entstehenden Zeitkomplexität von 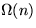 für die Suchoperation
IsElement
.
für die Suchoperation
IsElement
.
Operationen auf AVL-Bäumen:
- 1.
- IsElement
: Diese Operation wird wie bei den natürlichen Suchbäumen implementiert.
Wie oben ausgeführt, haben aber AVL-Bäume mit n Datenelementen eine Höhe von
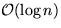 , woraus logarithmische Zeit für das Suchen folgt.
, woraus logarithmische Zeit für das Suchen folgt. - 2.
- Insert
:
Zunächst wird eine
IsElement
-Operation ausgeführt, die für den Fall, daß das einzufügende
Element nicht bereits enthalten ist, zu einem Blatt führt. Dies ist die Stelle, an der das neue
Element einzufügen ist. Dabei ergeben sich 2 Fälle:
1. Fall:
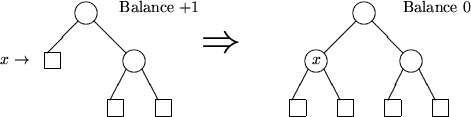
(Balance 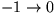 : symmetrisch)
: symmetrisch)
2. Fall:
Hier ist eventuell eine Rebalancierung auf dem Pfad zur Wurzel notwendig, denn die Höhe eines Unterbaums ändert sich derart,
daß die Balance nicht zu wird, sondern zu +1 oder -1. Zur Rebalancierung (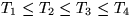 ):
):
Fall 2-a)
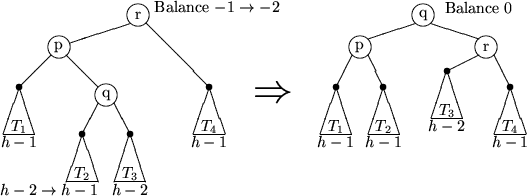
Fall 2-b)
- 3.
- Delete
: Auch diese Operation wird wie bei natürlichen Suchbäumen implementiert. Doch am Ende hat ggf. noch eine Rebalancierung
auf dem Pfad vom gelöschten Blatt (das an die Stelle des zu löschenden Elements geschrieben wird) zur Wurzel zu erfolgen.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Bei AVL-B\uml {a}umen sind die Operati...
...space die Anzahl der Datenelemente (oder die Anzahl
der Bl\uml {a}tter) ist.
}}](img186.gif)
Siehe auch:
- Aho, Hopcroft, Ullmann
- Sedgewick/Flajolet
- Info IV Skript SS94, Prof. Mayr
In der Theorie: Sehr schöne Eigenschaften.
In der Praxis: Sehr aufwendig zu implementieren.




Next: Hashing
Up: Binäre Suchbäume
Previous: Natürliche binäre Suchbäume
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
ist ein spezieller binärer Suchbaum, der neben den Sortierungsbedingungen auch die folgende Höhenbalancierungen erfüllt. Für den Knoten v gilt:
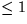
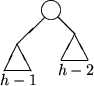
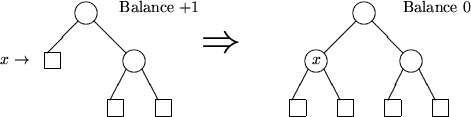
![]() : symmetrisch)
: symmetrisch)
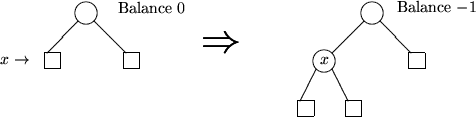
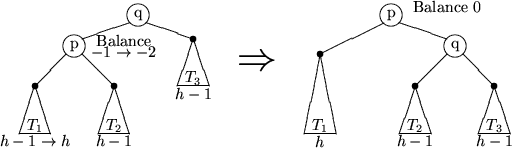
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Bei AVL-B\uml {a}umen sind die Operati...
...space die Anzahl der Datenelemente (oder die Anzahl
der Bl\uml {a}tter) ist.
}}](img186.gif)