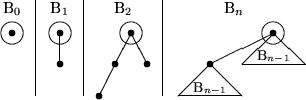
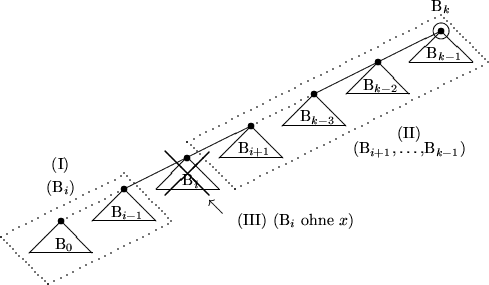
Definition: Die Binomialbäume sind rekursive wie folgt definiert:Achtung: Binomialbäume sind keine Binärbäume! Wie in folgender Darstellung dieser Bäume deutlich wird, hat Bn an der Wurzel Grad n.

(2)
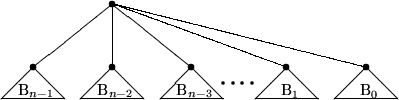
![\begin{picture}
(100,50)
\put(0,5){\circle*{2}}
\put(0,0){\makebox(10,5){B$_0$...
...7.5){\makebox(23,5)[r]{R''uckgrat}}
\put(35,40){\vector(4,-1){20}}\end{picture}](img237.gif)
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Es gilt:
\begin{enumerate}
\item $B_...
...tem $B_n$\space hat $\binom{n}{i}$\space Knoten in Tiefe $i$
\end{enumerate}}}](img238.gif)
Definition: Eine Binomial Queue mit N Elementen wird wie folgt aufgebaut:Beachte, daß Priority-Queues wegen
- 1.
- Betrachte die Binärdarstellung bin(N) von N
- 2.
- Für jedes gesetzte Bit (``1``) an Position i wird ein Binomialbaum vom Type Bi benötigt. Dieser hat bekanntlich 2i Knoten
- 3.
- Verbinde die Binomialbäume in einer doppelt verketteten zirkulären
Liste.- 4.
- Beachte, daß innerhalb jedes Binomialbaums die Minimumsvariante der Heap-Bedingung, nämlich VATER
SOHN erfüllt sein muß. Dadurch ist die Wurzel eines einzelnen Binomialbaums gleichzeitig sein minimales Element.
- 5.
- Richte einen Min-Pointer auf das Element in der Wurzel-Liste mit minimalem Schlüssel. Es ist dann das kleinste Element von allen in der Binomial Queue
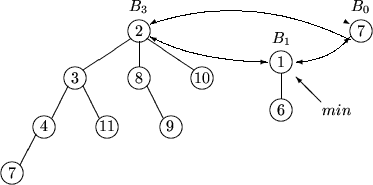
Beispiel: N=11 =(1011)2:
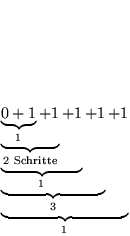
Komplexität: Binomial Queue Nr. 1 mit N1 Elementen hatfor i:= 0,1,2,3,.. do if
genau 3 Bis) then erzeuge/verbinde Bi+1 nach (*) und behalte ein Bi; elseif
genau 2 Bis) then erzeuge Bi+1 nach (*) ; elsif
ein Bi) then behalte es; fi od
| 1 | 1 | 1 | 1 | ||||
| (B7) | (B4) | (B2) | (B0) | ||||
| 1 | |||||||
| 1 | 1 | 1 | 1 | 1 |
| n | an |
| 1 | 2 |
| ..4 | 1 3 |
| ..8 | 1 2 1 4 |
| ..16 | 1 2 1 3 1 2 1 5 |
| ..32 | 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 6 |
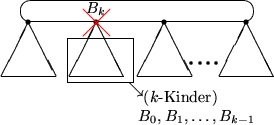
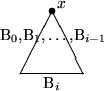
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Binomial-Queues haben f\uml {u}r die O...
...{\textsf{Initialize}}
worst-case-Kosten von jeweils $\mathcal{O}(\log{n})$.
}}](img270.gif)