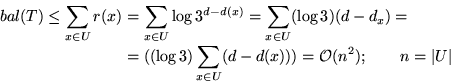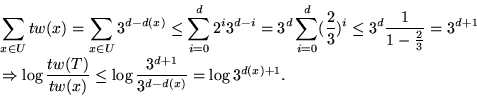![\begin{picture}
(118,24.5) %Hoehe ist absichtlich um 5 Einheiten zu klein gewaeh...
...ut(90.5,22.5){\circle*{2}}
\put(80.5,24.5){\makebox(10,5)[b]{$x$}}\end{picture}](img350.gif)
![]()
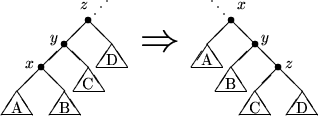
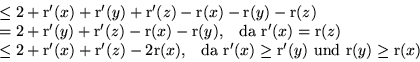
![]()
![]()
![]()
![]()
![\begin{picture}
(20,20)
\put(5,5){\vector(1,0){15}}
\put(5,5){\vector(0,1){15}...
...$}}
\put(10,10){\circle*{2}}
\put(11,11){\makebox(10,5)[bl]{max}}\end{picture}](img359.gif)
Beweis:
Da die Funktion z ![]() streng monoton wachsend ist, kann sich
das Maximum der Funktion f
streng monoton wachsend ist, kann sich
das Maximum der Funktion f![]() nur auf dem Geradensegment
x+y=1, x,y>0 befinden. Dadurch erhalten wir ein neues
Maximierungsproblem für die Funktion g
nur auf dem Geradensegment
x+y=1, x,y>0 befinden. Dadurch erhalten wir ein neues
Maximierungsproblem für die Funktion g![]() auf diesem
Geradensegment. Da g(x) an den Rändern gegen
auf diesem
Geradensegment. Da g(x) an den Rändern gegen ![]() strebt, muß es
sich um ein lokales Maximum handeln. Die einzige Nullstelle der Ableitung
strebt, muß es
sich um ein lokales Maximum handeln. Die einzige Nullstelle der Ableitung
![]()
![]()
Damit gilt:
![]()
![]()
![\begin{picture}
(115,37)
\put(7.5,0){\line(2,3){5}}
\put(7.5,0){\line(1,0){10...
...put(102.5,15){\circle*{2}}
\put(104.5,13.5){\makebox(3,5)[l]{$z$}}\end{picture}](img341.gif)
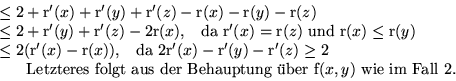
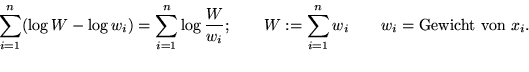
![% latex2html id marker 9247
\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $\text...
...\
\log\left(\frac{m}{\text{q}(i)}\right)\right)
\end{split} \end{equation*}}}](img380.gif)
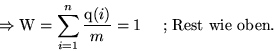
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Betrachte Folge von Zugriffsoperatione...
... (anfangs beliebigen) Splay-Tree f\uml {u}r die
Menge $\mathcal{O}(t+n^2)$.
}}](img383.gif)