



Next: k-Level-Buckets
Up: Buckets
Previous: 1-Level-Backets
Bei einem großen Wertebereich der zu speichernden Schlüssel, das heißt beim großen C, und einer
geringen Anzahl tatsächlich abgelegter Datenelemente sind 1-Level-Buckets in zweifacher Hinsicht ungünstig:
- Das Array b belegt statisch Speicherplatz der Größe
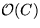 , obwohl nur ein kleiner
Teil davon wirklich gebraucht wird.
, obwohl nur ein kleiner
Teil davon wirklich gebraucht wird.
- Der Zeitbedarf für ein
ExtractMin
nähert sich der worst-case-Komplexität
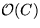 ,da der nächste nicht-leere Bucket ziemlich weit entfernt sein kann.
,da der nächste nicht-leere Bucket ziemlich weit entfernt sein kann.
2-Level-Buckets versuchen dem mit folgender Idee abzuhelfen: Verwende statt eines Arrays der
Länge C+1 zwei Arrays der Länge:
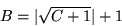
Dabei enthält eines der beiden Arrays die meisten Elemente in grob vorsortierter Form, nur die
Elemente mit den kleinsten Schlüsseln werden in dem zweiten Array dann endgültig sortiert vorgehalten.
2-Level-Buckets können mit folgenden Elementen aufgebaut werden:
- Das Array btop ([0..B-1]) nimmt in jedem Bucket Elemente mit
Schlüsseln aus einem Intervall der Länge B auf; die Schlüssel stammen
aus allen Intervallen außer dem niedrigsten Intervall.
- Das Array bbot ([0..B-1]) nimmt in jedem Bucket Elemente mit
genau einem Schlüssel auf; die Schlüssel stammen nur aus
dem niedrigsten.
- valtop ist die linke Intervallgrenze des niedrigsten Intervalls.
- postop enthält den Index des Buckets in btop für das niedrigste
Intervall (das aber in bbot gespeichert wird).
- nbot ist die Anzahl der Elemente in bbot
- n ist die Anzahl der Elemente in bbot und btop
Dabei gilt:
-
![$btop[(postop+1) \text{ mod } B]$](img413.gif) enthält alle Elemente x mit:
enthält alle Elemente x mit:
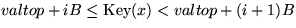
, wobei
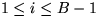
- bbot[i] enthält alle Elemente x mit
Key(
x) =
valtop +
i, wobei
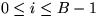
Dazu ist allerdings folgende Annahme zu machen:
Hat ein
ExtractMin
ein Element mit Schlüssel k zurückgeliefert, werden bis zum nächsten
Aufruf von
ExtractMin
nur Elemente mit Schlüsseln 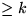 und
und 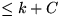 eingefügt. Dies
stellt sicher, daß ein Element aus bbot nie nach btop wandert.
eingefügt. Dies
stellt sicher, daß ein Element aus bbot nie nach btop wandert.
Lemma:
Zu jedem Zeitpunkt haben alle Schlüssel Platz in der Datenstruktur.
Beweis: Am meisten Platz wird benötigt, wenn der kleinste Schlüssel ganz rechts in bbot
gespeichert oder dort entfernt worden ist. Er hat dann den Wert valtop + B -1. Der größte
Schlüssel, der nun vorkommen kann und also Platz finden muß, ist valtop + B -1 +C:


Annahme: Vor dem ersten
ExtractMin
werden nur Elemente mit 0 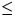 Schlüssel
Schlüssel
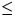 C eingefügt.
C eingefügt.
- i)
- Initialize
:
valtop = postop = nbot = n = 0;
Initialisiere bbot, btop;
- ii)
- Insert(x)
:
überprüfe Invarianten;
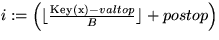 mod B;
if i== postop then
Füge x in bbot[Key(x)-valpop] ein;
nbot:= nbot + 1 ; n:=n+1;
else
Füge x in btop[i] ein;
fi
mod B;
if i== postop then
Füge x in bbot[Key(x)-valpop] ein;
nbot:= nbot + 1 ; n:=n+1;
else
Füge x in btop[i] ein;
fi
- iii)
- ExtractMin
co suche kleinste Element in bbot oc
j:=0 ; while ![$bbot[j] ==\emptyset$](img421.gif) do j:=j+1 od
entferne ein (beliebiges) Element aus bbot[j] und gib es zurück;
nbot := nbot -1 ; n := n -1;
if n==0 then return fi
if nbot==0 then
while
do j:=j+1 od
entferne ein (beliebiges) Element aus bbot[j] und gib es zurück;
nbot := nbot -1 ; n := n -1;
if n==0 then return fi
if nbot==0 then
while ![$btop[postop]==\emptyset$](img422.gif) do
postop:=(postop+1) mod B;
valtop:=valtop + B;
od
while
do
postop:=(postop+1) mod B;
valtop:=valtop + B;
od
while ![$btop[postop]\neq\emptyset$](img423.gif) do
entferne beliebiges Element x aus btop[postop];
Füge x im bbot[Key(x)-valtop] ein;
nbot:=nbot+1;
od
fi
do
entferne beliebiges Element x aus btop[postop];
Füge x im bbot[Key(x)-valtop] ein;
nbot:=nbot+1;
od
fi
- iv)
- DecreaseKey(x,k)
enferne x aus seinem momentanen Bucket;
falls nötig, aktualisiere nbot
Key(x) := k;
Insert(x);
Lemma:
Worst-case (reelle) Laufzeit bei 2-Level Buckets sind für
Insert
und
DecreaseKey
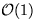 , für
ExtractMin
, für
ExtractMin
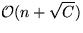 und
und 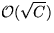 (bzw.
(bzw. 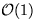 ) für
Initialize
.
) für
Initialize
.
Beweis:
-
Insert
: 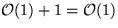
-
DecreaseKey
: 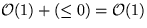
-
ExtractMin
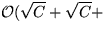 # Elemente
# Elemente 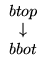 ).
).

Potential: Anzahl von Elementen im Buckets im btop.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Amortisierte Kosten f\uml {u}r 2-Level...
...ey}}
und
$\mathcal{O}(\sqrt{C})$\space bei
\textsl{\textsf{ExtractMin}}
.
}}](img430.gif)
Beweis:
-
Insert
: s.o.
-
DecreaseKey
: s.o.
-
ExtractMin
: 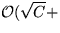 # Elemente
# Elemente 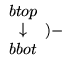 # Elemente
# Elemente 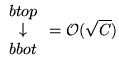





Next: k-Level-Buckets
Up: Buckets
Previous: 1-Level-Backets
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]()
![\begin{picture}
(160,148)
\small
\put(50,110){
\framebox
(9.8,10)[tr]{0}}
\put(...
...0}}
\put(105,40){\vector(0,-1){10}}
\put(125,40){\vector(0,-1){10}}\end{picture}](img412.gif)

mod B; if i== postop then Füge x in bbot[Key(x)-valpop] ein; nbot:= nbot + 1 ; n:=n+1; else Füge x in btop[i] ein; fi
do j:=j+1 od entferne ein (beliebiges) Element aus bbot[j] und gib es zurück; nbot := nbot -1 ; n := n -1; if n==0 then return fi if nbot==0 then while
do postop:=(postop+1) mod B; valtop:=valtop + B; od while
do entferne beliebiges Element x aus btop[postop]; Füge x im bbot[Key(x)-valtop] ein; nbot:=nbot+1; od fi
![]() , für
ExtractMin
, für
ExtractMin
![]() und
und ![]() (bzw.
(bzw. ![]() ) für
Initialize
.
) für
Initialize
.
![]()
![]()
![]() # Elemente
# Elemente ![]() ).
).
![]()
![]()
![]() # Elemente
# Elemente  # Elemente
# Elemente 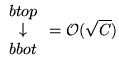
![]()