



Next: Generischer minimaler Spannbaum-Algorithmus
Up: Minimale Spannbäume
Previous: Minimale Spannbäume
Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen(Tarjan):
- ,,blaue`` Regel
- ,,rote`` Regel
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $G=(V,E)$\space ein zusammenh\uml ...
...malen Spannbaum von $(G,$w$)$, der $e$\space enth\uml {a}lt.
\end{enumerate}}}](img815.gif)
Beweis: durch Widerspruch
- 1.
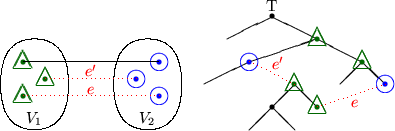
- Sei T ein minimaler Spannbaum von (G,w), sei
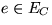 die minimale Kante.
Annahme:
die minimale Kante.
Annahme: 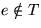 . Da T Spannbaum
. Da T Spannbaum 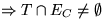 .
.
Sei 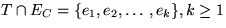 . Dann
enthält
. Dann
enthält  einen eindeutig bestimmten Kreis (den
sogenannten durch e bzgl. T bestimmten Fundamentalkreis).
Dieser Kreis muß mindestens eine Kante
einen eindeutig bestimmten Kreis (den
sogenannten durch e bzgl. T bestimmten Fundamentalkreis).
Dieser Kreis muß mindestens eine Kante 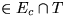 enthalten, da die beiden
Endpunkte von e auf verschiedenen Seiten des Schnitts C liegen.
Sei
enthalten, da die beiden
Endpunkte von e auf verschiedenen Seiten des Schnitts C liegen.
Sei 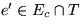 . Dann gilt nach Vorraussetzung w(e') >w(e).
Also ist
. Dann gilt nach Vorraussetzung w(e') >w(e).
Also ist 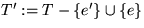 ein Spannbaum von G, der echt
kleineres Gewicht als T hat, Widerspruch zu T ist minimaler Spannbaum.
ein Spannbaum von G, der echt
kleineres Gewicht als T hat, Widerspruch zu T ist minimaler Spannbaum.
- 2.
- Sei
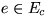 minimal. Annahme: e kommt in keinem
minimalen Spannbaum vor. Sei T ein beliebiger minimaler Spannbaum von (G,w).
minimal. Annahme: e kommt in keinem
minimalen Spannbaum vor. Sei T ein beliebiger minimaler Spannbaum von (G,w).
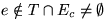 . Sei
. Sei 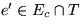 eine Kante auf dem durch e bezüglich T
erzeugten Fundamentalkreis. Dann ist
eine Kante auf dem durch e bezüglich T
erzeugten Fundamentalkreis. Dann ist 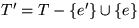 wieder ein
Spannbaum von G, und es ist w
wieder ein
Spannbaum von G, und es ist w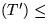 w(T). Also T' minimaler Spannbaum und
w(T). Also T' minimaler Spannbaum und
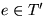 .
.

![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $G=(V,E)$, $w:E\to\mathbbm{R}$, ei...
... minimalen
Spannbaum, der $e_i$\space nicht enth\uml {a}lt.
\end{enumerate}}}](img831.gif)
Beweis:
- 1.
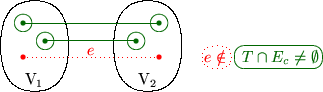
- Nehmen wir an, daß es einen minimalen Spannbaum T gibt,
der
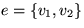 enthält. Wenn wir e aus T entfernen, so
zerfällt T in zwei nicht zusammenhängende Teilbäume T1 und T2
mit
enthält. Wenn wir e aus T entfernen, so
zerfällt T in zwei nicht zusammenhängende Teilbäume T1 und T2
mit  , i=1,2. Da aber e auf einem Kreis in G liegt,
muß es einen Weg von v1 nach v2 geben, der e nicht benützt.
Mithin gibt es eine Kante
, i=1,2. Da aber e auf einem Kreis in G liegt,
muß es einen Weg von v1 nach v2 geben, der e nicht benützt.
Mithin gibt es eine Kante 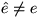 auf diesem Weg, die einen
Knoten in T1 mit T2 verbindet. Verbinden wir T1 und T2
entlang
auf diesem Weg, die einen
Knoten in T1 mit T2 verbindet. Verbinden wir T1 und T2
entlang 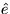 , so erhalten wir einen von T verschiedenen
Spannbaum
, so erhalten wir einen von T verschiedenen
Spannbaum 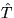 . Wegen
. Wegen 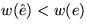 folgt
folgt 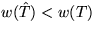 . Ein Widerspruch.
. Ein Widerspruch.
- 2.
- Wir nehmen an, ei liege in jedem minimalen Spannbaum (MSB) von G, und
zeigen die Behauptung durch Widerspruch.
Sei T ein beliebiger MSB von G. Entfernen wir ei
aus T, so zerfällt T in zwei nicht zusammenhängende Teilbäume T1
und T2. Da ei auf einem Kreis 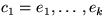 in G liegt,
können wir wie unter 1. ei durch eine Kante ej des Kreises c1
ersetzen, die T1 und T2 verbindet.
Dadurch erhalten wir einen von T verschiedenen Spannbaum
in G liegt,
können wir wie unter 1. ei durch eine Kante ej des Kreises c1
ersetzen, die T1 und T2 verbindet.
Dadurch erhalten wir einen von T verschiedenen Spannbaum
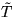 , der ei nicht enthält. Da nach Voraussetzung
, der ei nicht enthält. Da nach Voraussetzung 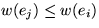 gilt, folgt
gilt, folgt 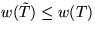 (und sogar
(und sogar 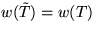 , da
T nach Annahme ein MSB ist). Also ist
, da
T nach Annahme ein MSB ist). Also ist 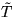 ein MSB von G,
der ei nicht enthält, im Widerspruch zur Annahme, ei liege in
jedem MSB von G.
ein MSB von G,
der ei nicht enthält, im Widerspruch zur Annahme, ei liege in
jedem MSB von G.

Literatur: R.E. Tarjan: ``Data Structures and Network Algorithms'',
SIAM CBMS-NSF Reihe Bd. 44.




Next: Generischer minimaler Spannbaum-Algorithmus
Up: Minimale Spannbäume
Previous: Minimale Spannbäume
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $G=(V,E)$\space ein zusammenh\uml ...
...malen Spannbaum von $(G,$w$)$, der $e$\space enth\uml {a}lt.
\end{enumerate}}}](img815.gif)


![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $G=(V,E)$, $w:E\to\mathbbm{R}$, ei...
... minimalen
Spannbaum, der $e_i$\space nicht enth\uml {a}lt.
\end{enumerate}}}](img831.gif)