Next: Das single-source-shortest-path-Problem Up: Kürzeste Pfade Previous: Kürzeste Pfade

Grundlegende Begriffe

Betrachte Digraph G=(V,A) oder Graph G=(V,E).

$\begin{picture} (72,27) \put(0,10){\makebox(25,0){Kante von}} \put(0,6){\makebox... ...,20) \put(40,18){\vector(0,1){1.5}} \put(70,22){\vector(0,-1){1.5}}\end{picture}$

Distanzfunktion:

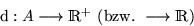
$\begin{displaymath} \text{d}: A \longrightarrow \mathbbm{R}^+ \text{ (bzw. } \longrightarrow \mathbbm{R}\text{)}\end{displaymath}$

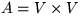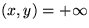O.B.d.A.: $A=V\times V$ , d $(x,y)=+\infty$ für Kanten, die eigentlich nicht vorhanden sind.
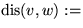$\text{dis}(v,w):=$ Länge eines kürzesten Pfades von v nach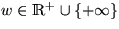 $w \in \mathbbm{R}^+ \cup \{+ \infty \}$

Arten von kürzeste-Pfade-Problemen:

1.: single-pair-shortest-path ( spsp ). Beispiel: Kürzeste Entfernung von München nach Frankfurt.
2.: single-source-shortest-path: gegeben G, d und 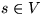$s \in V$ , bestimme für alle 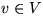$v\in V$ die Länge eines kürzesten Pfades von s nach v (bzw. einen kürzesten Pfad von s nach v) ( sssp ). Beispiel: Kürzeste Entfernung von München nach allen anderen Großstädten.
3.: all-pairs-shortest-path ( apsp ) . Beispiel: Kürzeste Entfernung zwischen allen Großstädten.

Bemerkung: Es gibt keinen Algorithmus, der das single-pair-shortest-path berechnet, ohne nicht gleichzeitig das single-source-shortest-path-Problem zu lösen.

Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999