Grundsätzliches

Next: Modifikation von Bellman-Ford-Algorithmus Up: Digraphen mit negativen Kantengewichten Previous: Digraphen mit negativen Kantengewichten

Grundsätzliches

Betrachte Startknoten s und einen Kreis C mit Gesamtlänge <0 und C ist von s aus erreichbar.

$\begin{picture} (120,40) \put(5,20){\circle*{2}} \put(20,20){\circle*{2}} ... ... \put(67,30){\makebox(0,0){$-5$}} \put(80,20){\makebox(0,0){$C$}}\end{picture}$

Sollte ein Pfad von s nach C und von C nach v existieren, so ist der kürzeste Pfad nicht definiert. Falls aber die Gesamtlänge des Kreises 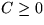$C\geq 0$ ist,

$\begin{picture} (120,40) \put(5,20){\circle*{2}} % \put(20,20){\circle*{2}} ... ... \put(92,30){\makebox(0,0){$1$}} \put(67,30){\makebox(0,0){$-3$}}\end{picture}$

dann ist der kürzeste Pfad wohl definiert. Probleme gibt es also nur dann, wenn es einen Zyklus negativer Länge gibt. Nichtsdestotrotz funktioniert Dijkstra-Algorithmus bei negativen Kantenlängen nicht.

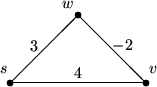
$\begin{picture} (50,30) \put(5,5){\circle*{2}} \put(25,25){\circle*{2}} \pu... ...} \put(38,16){\makebox(0,0){$-2$}} \put(25,8){\makebox(0,0){$4$}}\end{picture}$

Bei diesem Beispielgraphen (der nicht einmal einen negativen Kreis enthält) berechnet der Dijkstra-Algorithmus die minimale Entfernung von s nach w fälchlicherweise als 3 (statt 2).

Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999