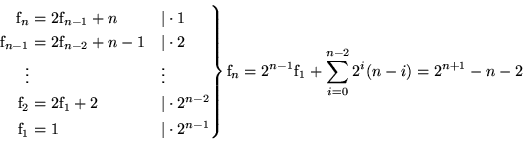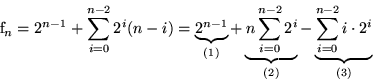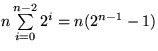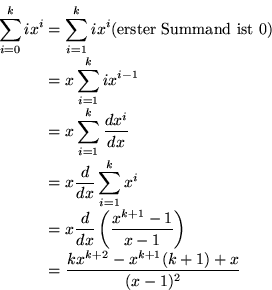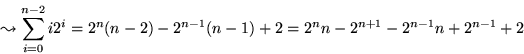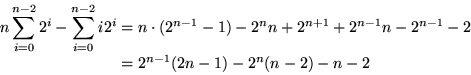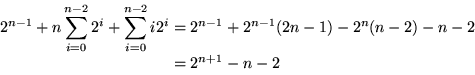Next: Charakteristisches Polynom
Up: Rekursionsgleichungen
Previous: Rekursionsgleichungen
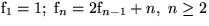 ;
;
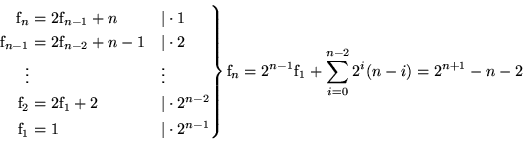
Addieren aller Gleichungen:
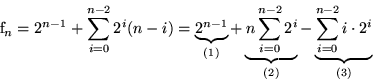
(2) (Geometrische Reihe): 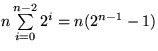
(3) (Substitution: n-2=k):
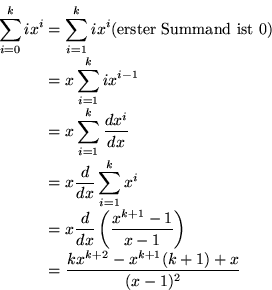
Einsetzen von k=n-2 und x=2:
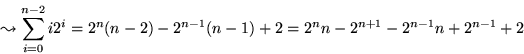
(2)-(3):
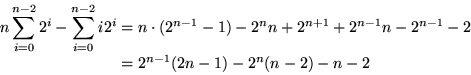
(1)+(2)-(3):
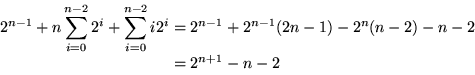
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]() ;
;