
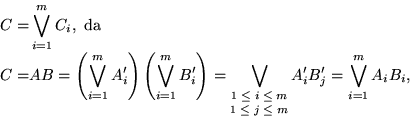
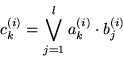
comb
;for j:=1 to
do
; co p Index der vordersten 1 von j oc comb[j]:=comb
od
Beispiel:
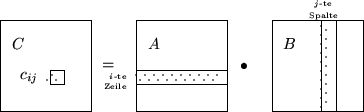
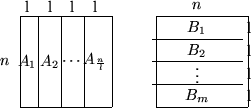
co die Matrizen a,b,c sind als Vektor von n Zeilenvektoren organisiert oc const
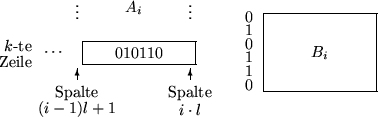
co wir nehmen l|n an oc; array comb[0..2l-1] of boolean-vector; for i:=1 to n do
od for i:=1 to
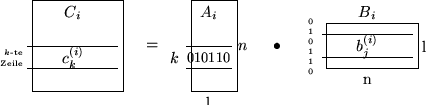
do co Berechne die Ci's oc bcomb(i); for j:=1 to n do co Bitmuster in der j-ten Zeile von Ai in Binärzahl wandeln oc nc:=0; for
downto
do if a[j,k] then nc:=nc+nc+1 else nc:=nc+nc fi od
comb[nc]; od od
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Der 4-Russen Algorithmus berechnet das...
...w. mit $\mathcal{O}\left(\frac{n^2}{\log n}\right)$\space Vektoroperationen.
}}](img1085.gif)