(a,b)-Bäume

Definition: Ein (a,b)-Baum ist ein externer Suchbaum, alle Blätter haben die gleiche Tiefe, die Anzahl der Kinder eines jeden internen Knoten ist $\leq$ b und $\geq$ a (Für die Wurzel $\geq 2$), und es gilt $b \geq 2a-1$.Spezialfall: b=2a-1 (B-Bäume).

Mit jedem internen Knoten V mit d=Grad(V) werden (d+1) Schlüsselwerte $K_0,\dots,K_d$ gespeichert.
$K_0=-\infty$, $K_d=+\infty$ , K_i-1 < (alle Schlüssel im i Unterbaum von V ) $\leq K_d$
etwa (*): k_i= max(Schlüssel im i-ten UB von V)

Sortierung im (a,b)-Baum:

(Schlüssel im i-ten UB) $\leq$ (Schlüssel im (i+1)-ten UB)

Beispiel:

Wir betrachten im folgenden (2,4)-Bäume.

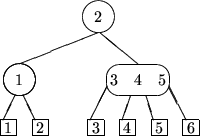
Lemma: Sei T ein (a,b)-Baum mit n Blättern und der Höhe h. Dann gilt:

$$\begin{split} (1) & \quad 2a^{h-1} \leq n \leq b^h\\ (2) &... ...\log n}{\log b} \leq h \leq 1+\log_a{\frac{n}{2}} \end{split}$$

Beweis:

(1)

$n \leq b^h$: Maximal für vollständigen Baum-Verzweigungsgrad b. Minimal für Baum mit Grad der Wurzel = 2, alle anderen internen Knoten = a.

(2)

aus (1).

$\Diamond$

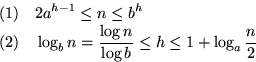
Operationen:

1.

IsElement(K,S)

v := Wurzel von T;
while $v \neq$ Blatt do
		 $i = \min\{ s \vert 1 \leq s \leq \text{Grad } v \text{ and } K\leq K_S \}$;  		 $v:=i\text{-tes Kind von }v$;  
od;
if K =Key(v) then return Val(k)
else return False 
fi;         

2.

Insert(K,S)

Führe    IsElement(K,T) aus. $\leadsto$ Blatt w;
Sei Key($w) \neq K$, w enthält unter (*) den kleinsten Schlüssel > K; 
Füge K links von w ein; 
v=Vater von w;
Falls Grad v=b+1: Rebalancierung (v);

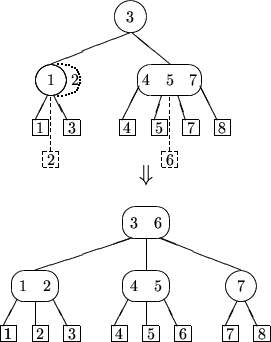
Rebalancierung(v):

a)

Falls ein unmittelbarer Bruder v' von v Grad < b hat, v' adoptiert äußerstes links/rechts Kind von v.

b)

Sonst: Spalte Menge C aller Kinder von v in C₁,C₂ ($\sim$gleichgroß). Spalte Knoten v in v₁,v₂,v₁ übernimmt C₁, v₂ übernimmt C₂;
$a\leq \lfloor \frac{b+1}{2} \rfloor \leq \lceil \frac{b+1}{2}\rceil \leq b$ wegen $b \geq 2a-1$

3.

Delete(x,S) :

Führe    IsElement(K,T) aus. $\leadsto$ Blatt w. Sei Key(w) = K;
Lösche w; v:= Vater w;
Falls Grad v=a-1: Rebalancierung'(v);

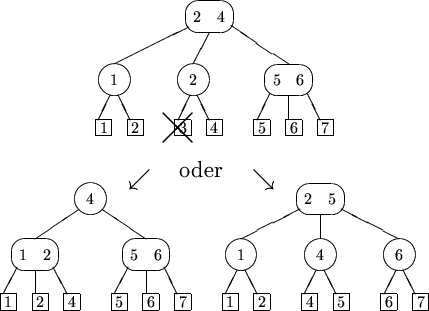
Rebalancierung'(v):

a)

Falls ein unmittelbarer Bruder v' von v Grad > a hat: v adoptiert Kind von v'

b)

Sonst verschmelze v mit einem unmittelbaren Bruder

Spezialfälle von (a,b)-Bäume:

-

(2,3)-Bäume,

-

(2,4)-Bäume,

-

(a,2a-1)-Bäume (B-Bäume)

Bemerkungen:

1.

Zur Wahl von a:

• Daten in RAM $\Rightarrow a$ klein, z.B. a=2 oder a=3.
• Daten auf Platte $\Rightarrow a$ groß, z.B. a=100.

2.

Zur Wahl von b:
$b \geq 2a$ liefert wesentlich bessere amortisierte Komplexität (ohne Beweis, siehe Mehlhorn).

3.

Top-Down-Rebalancierung: $b \geq 2a$.
Bei der Restrukturierung nach der Top-Down-Strategie, folgen wir wie gewohnt dem Pfad von der Wurzel zum gesuchten Blatt. Beim Einfügen stellen wir jetzt jedoch für jeden besuchten Knoten sicher, daß der Knoten weniger als b Kinder hat. Wenn der gerade betrachtete Knoten ein b-Knoten ist, dann spalten wir ihn sofort auf. Weil der Vater kein b-Knoten ist (das haben wir ja bereits sichergestellt) pflanzt sich der Aufspaltungsprozeß nicht nach oben hin fort. Insbesondere kann das neue Element ohne Probleme eingefügt werden, wenn die Suche das Blattniveau erreicht hat. Damit diese Strategie möglich ist, muß b mindestens 2a sein (und nicht 2a-1), da sonst nach der Spaltung nicht genügend Elemente für die beiden Teile vorhanden sind.
Beim Löschen verfahren wir analog. Für jeden besuchten Knoten, außer der Wurzel des (a,b)-Baumes, stellen wir sicher, daß er mindestens a+1 Kinder hat. Wenn der gerade betrachtete Knoten nur a Kinder hat, so versuchen wir zuerst ein Element des rechten oder linken Nachbarknoten zu stehlen. Sind beide Nachbarknoten vom Grad a, so verschmelzen wir unseren Knoten mit einem der beiden Nachbarn. Ist der Vater nicht die Wurzel, so hatte er aber vorher mindestens a+1 Kinder, und dieser Verschmelzungsprozeß kann sich nicht nach oben fortsetzen. Andernfalls erniedrigt sich der Grad der Wurzel um 1, wenn die Wurzel Grad größer 2 hat, oder die alte Wurzel wird gelöscht und der soeben verschmolzene Knoten wird zur neuen Wurzel.
Restrukturierung nach der Top-Down-Strategie sorgt nicht für eine bessere Laufzeit, sondern erleichtert die Synchronisation, wenn mehrere Prozesse gleichzeitig auf einen (a,b)-Baum zugreifen wollen. Bei herkömmlichen (a,b)-Bäumen schreiten die Such- und die Restrukturierungsoperationen in entgegengesetzten Richtungen fort, was dazu führt, daß sich oft Prozesse gegenseitig behindern (der eine will im Baum absteigen, der andere muß auf dem gleichen Pfad aufwärts restrukturieren). Bei der Top-Down-Strategie gibt es nur Operationsfolgen, die den Baum hinabsteigen. Mehrere Prozesse können so in einer Art Pipeline gleichzeitig einen Pfad mit kurzem Abstand begehen.