Rot-Schwarz-Bäume

Next: Binäre Suchbäume Up: Höhenbalancierte Bäume Previous: (a,b)-Bäume

Rot-Schwarz-Bäume

Definition: Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so daß gilt:

1.
alle Blätter hängen an schwarzen Kanten (durchgezogene Linien)
2.
alle Blätter haben die gleiche ,,Schwarztiefe``
3.
kein Pfad von der Wurzel zu einem Blatt enthält aufeinanderfolgende rote Kanten (gewellte Linien).

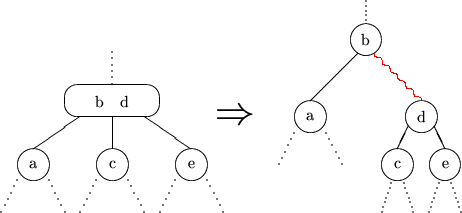
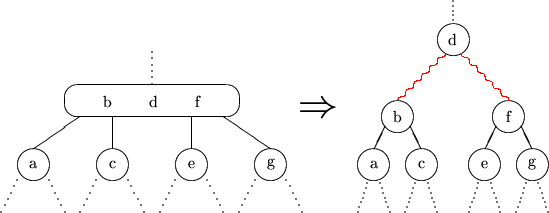
Dabei ist die ,,Schwarztiefe`` eines Knoten die Anzahl der schwarzen Kanten auf dem Pfad von der Wurzel zu diesem Knoten. Rot-Schwarz-Bäume können zur Implementierung von (2,4)-Bäumen dienen.
Vorteil: Interne Knoten haben Verzweigungsgrad =2.

$\begin{picture} (108,70) \multiput(0,0)(1,2){6}{\circle*{0.1}} \multiput(20,0)... ...,2){6}{\circle*{0.1}} \multiput(115,60.5)(0,1.5){5}{\circle*{0.1}}\end{picture}$

$\begin{picture} (173,70) \multiput(0,0)(1,2){6}{\circle*{0.1}} \multiput(20,0)... ... \color {black} \multiput(142.5,60.5)(0,1.5){5}{\circle*{0.1}}\end{picture}$

Operationen auf Rot-Schwarz implementierten (a,b)-Bäume:

1.: IsElement(K,T) : vgl. (a,b)-Bäume
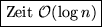
$\fbox {Zeit $\mathcal{O}(\log n)$}$
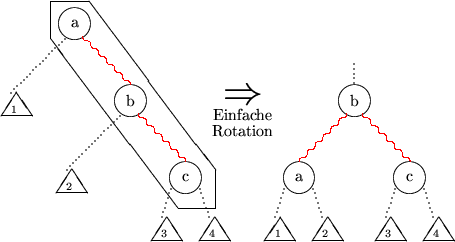
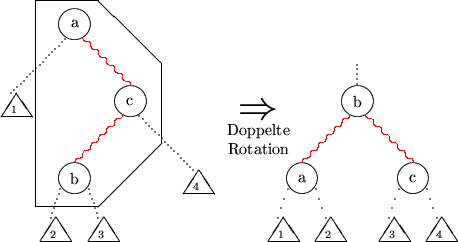
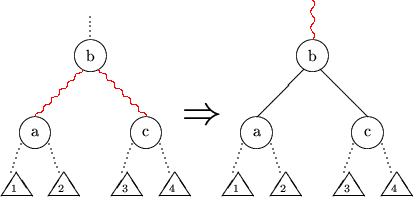
2.: Insert(K,T) : Führe IsElement(K,T) aus $\leadsto$ Blatt w. Dort sei noch nicht das Element v gespeichert. Ersetze w durch interne Knoten w' mit Kindern v,w, wobei v ein neues Blatt mit Schlüssel K sei. w' behält rote Eingangskante. Falls nun zwei aufeinanderfolgende rote Kanten an w' vorliegen, Rotation zur Rebalancierung:

$\begin{picture} (144,76) \put(83.25,0){ \usebox {\ubaumbox} } \put(83.25,0){... ... \put(69.5,10.3){\line(-1,0){12}} \put(57.5,10.3){\line(-3,4){40}}\end{picture}$

$\begin{picture} (145,80) \put(84.25,0){ \usebox {\ubaumbox} } \put(84.25,0){... ...0}} \put(32.5,76){\line(-1,0){20}} \put(12.5,76){\line(0,-1){65}}\end{picture}$

$\begin{picture} (120,65) \put(70,0){ \usebox {\ubaumbox} } \put(70,0){\makeb... ...5)} \color {black} \multiput(30,50.5)(0,1.5){5}{\circle*{0.1}}\end{picture}$
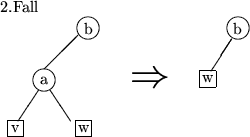
3.: Delete(K,T) : Das Löschen des Blattes v macht es erforderlich, daß der Vater des Blattes durch den Bruder des Blattes ersetzt wird, damit der Binärbaumstruktur erhalten bleibt. Der Bruder von v ist natürlich eindeutig bestimmt. Dabei treten zwei Fälle auf:

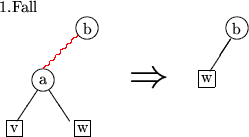
$\begin{picture} (115,60) \put(0,0){ \framebox (7,7){v}} \put(30,0){ \framebox ... ...ut(101.5,45.5){\makebox(5,5){b}} \put(0,55){\makebox(15,5){1.Fall}}\end{picture}$
:
Dadurch ändert sich die Schwarztiefe von w nicht, denn die Eingangskante zu w wird (notwendig) zu schwarz umgefärbt. Auch kann es hierdurch nicht zu zwei aufeinanderfolgenden roten Kanten kommen.

$\begin{picture} (115,60) \put(0,0){ \framebox (7,7){v}} \put(30,0){ \framebox ... ...ut(101.5,45.5){\makebox(5,5){b}} \put(0,55){\makebox(15,5){2.Fall}}\end{picture}$
Hierdurch verkleinert sich die Schwarztiefe von w um 1. Man kann sie nicht wieder erhöhen, ohne dabei auch die Schwarztiefe anderer Blätter zu vergrößern. Daher muß sie für alle anderen Blätter des Baumes um 1 verkleinert werden. Man betrachte dazu den Pfad von w zur Wurzel als unveränderlich und färbt Kanten so um, daß auf allen anderen Pfaden jeweils genau eine Kante von schwarz zu rot wird. Ferner darf dabei nicht die Situation entstehen, daß zwei aufeinanderfolgende Kanten rot werden. Ist dies nicht vermeidbar, so muß gemäß obigem Schema rebalanciert werden.

$\fbox {\parbox[c]{12.45cm}{\textbf{Satz:} Die Tiefe eines Rot-Schwarz-Baumes mit $n$\space Bl\uml {a}ttern ist $\mathcal{O}(\log n)$ }}$

Beweis: Siehe Übungsblatt. $\Diamond$

$\fbox {\parbox[c]{12.45cm}{\textbf{Korollar:} Die W\uml {o}rterbuch-Operationen ... ...uml {o}tigen auf Rot-Schwarz-B\uml {a}umen $\mathcal{O}(\log n)$\space Zeit. }}$

Next: Binäre Suchbäume Up: Höhenbalancierte Bäume Previous: (a,b)-Bäume

Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999