



Next: Hashing mit offener Adressierung
Up: Hashing
Previous: Grundlagen
Die Hashtabelle ist eine array von m linearen Listen, wobei die i-te Liste alle k
Schlüssel beinhaltet, für die gilt:
h(k)=i
Zugriff: Berechne h(k) und durchsuche die Liste T[h(k)].
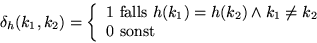
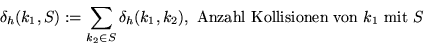
Zugriffskosten : 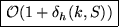
worst-case: h|s= const 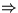 Entartung des Hashings zu linearer Suche
Entartung des Hashings zu linearer Suche 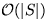
average-case :
- -
- Möge h das Universum U über [0..m-1] gleichverteilen
- -
- Seien alle Werte in U gleichwahrscheinlich als Argument von
Access()
,
Insert()
,
Delete()
- -
- Sei
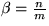 der maximale Füllgrad von T, n= Anzahl
Operationen
der maximale Füllgrad von T, n= Anzahl
Operationen
Dann: Die erwartete Laufzeit für n-Operationen =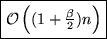
Beweis: Durch die Gleichverteilung für den Wert h(ki) bei der i-ten Operation
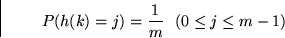
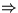
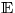 (Listenlänge)
(Listenlänge) 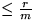 nach der r-ten Operation
nach der r-ten Operation
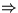
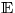 (Kosten von (n+1)-ten Operationen)
(Kosten von (n+1)-ten Operationen) 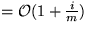
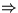
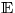 (Kosten von n Operationen)
(Kosten von n Operationen) 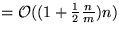

Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]()
![]()
![]()