Die Datenstruktur

• Die Schlüssel sind an den Knoten von Bäumen gespeichert
• Jeder Knoten hat
  • Schlüssel und Wert
  • Rang (Anzahl der Kinder)
  • Zeiger zum ersten Kind, zum Vater (NIL im Falle der Wurzel), doppelt verkettete Liste der Kinder
  • Markierung 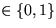$\in\{0,1\}$ (außer Wurzel)

Bemerkung: Die doppelte Verkettung der Kinder- bzw. Wurzellisten innerhalb von Heaps erlaubt das Löschen eines Listeneintrages in Zeit $\mathcal{O}(1)$.

Binomial-Queue vs. Fibonacci-Heap:

• Fibonacci-Heaps: Wald von Bäumen, innerhalb derer die Heap-Bedingungen erfüllt sind.
• A-Priori: Keine Einschränkung für die Topologie der Bäume, aber ohne

  Delete - oder DekreaseKey-Operation bleibt ein Binomialwald ein Binomialwald.

• keine Invariante der Form ``Nur Bäume verschiedenen Wurzel-Rangs``.

Überblick:

Operationen worst case amortisiert

$$\mathcal{O}(1) \mathcal{O}(1)$$

$$\mathcal{O}(1) \mathcal{O}(1)$$

$$\mathcal{O}(1) \mathcal{O}(1)$$

$$\mathcal{O}(\log{n}) \mathcal{O}(1)$$

$$\mathcal{O}(\log{n}) \mathcal{O}(\log{n})$$

$$\mathcal{O}(n) \mathcal{O}(\log{n})$$

Linken von Bäumen: Zwei Bäume desselben Wurzel-Rangs werden unter Einhaltung der Heap-Bedingung verbunden. Sind k₁ und k₂ die Wurzeln der zwei zu linkenden Bäume, so wird ein neuer Baum aufgebaut, dessen Wurzel bzgl. der Schlüssel das Minimum von k₁ und k₂ ist. Sei dies k₂, dann erhält der Baum mit Wurzel k₂ als zusätzlichen Unterbaum den Baum mit Wurzel k₁, d.h. der Rang von k₂ erhöht sich um eins.

Dies ist gerade der konstruktive Schritt beim Aufbau von Binomialbäumen. Zur Verbesserung der amortisierten Zeitschranken sind zusätzlich folgende Regel Formuliert:

Kaskadiertes Abschneiden:

• Ein Knoten ist im ``Anfangszustand``, wenn

  i)

  er durch einen Linkschritt Kind eines anderen Knotens wird oder

  ii)

  er in die Wurzelliste eingefügt wird.

• Wenn ein Knoten ab seinem Anfangszustand zum zweitenmal einen Sohn verliert, wird er in die Wurzelliste eingefügt.
• Der kritische Zustand (ein Kind verloren) wird durch das Markierungsbit angezeigt.

Algorithmus:

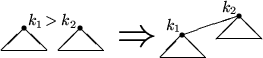
		 x verliert Kind;
		 y= P(x) : (Vater von x)
		 while (y markiert) do
		 		 entferne y;
		 		 füge y unmarkiert in die Liste ein;
		 		 if (P(y)=NIL) then exit fi
		 		 y= P(y);
		 od
		 markiere y;  

Operationen:

1.

Insert(x) : Füge B (mit dem Element x) in die Wurzelliste ein.
Update Min-Pointer.

2.

Merge() : Verbinde beide Listen und aktualisiere den Min-Pointer.

3.

FindMin() : Es wird das Element ausgegeben, auf das der Min-Pointer zeigt. Dabei handelt es sich sicher um eine Wurzel.

4.

Delete(x)

i)

Falls x Min-Wurzel, DeleteMin -Operator benutzen

ii)

Sonst:

while true do
		 füge Liste der Kinder in die Wurzelliste ein;
		 lösche x, x=Vater(x);
		 if Markierung(x)=0 then Markierung(x)=1 exit
		 else
		 		 hänge x samt Unterbaum in Wurzelliste;
		 		 entferne Markierung von x da x Wurzel;
		 		 x = Vater(x);
		 fi
od

5.

DeleteMin() : Diese Operation hat auch Aufräumfunktion und ist daher recht kostspielig. Sei x der Knoten, auf den der Min-Pointer zeigt:

		 $x:= \uparrow$ Min-Pointer;
		 entferne x aus der Liste;
		 Konkataniere Kinderliste vom x mit der Wurzelliste;
		 while ($\exists \geq 2$ Bäume von selben Wurzel-Rang i) do
		 		 erzeuge Baum vom Wurzel-Rang i+1;  		 od
		 update Min-Pointer; 

Man beachte, daß an jedem Knoten, insbesondere jeder Wurzel, der Rang gespeichert ist. Zwar vereinfacht dies die Implementierung, doch müssen noch immer Paare von Wurzeln gleichen Rangs gefunden werden. Dies wird wie folgt realisiert: Wir verwenden ein array, dessen Indizies je für einen Rang stehen. Die Elemente sind Zeiger auf eine Wurzel dieses Rangs. Es ist garantiert, daß ein Element nur dann unbesetzt ist, wenn tatsächlich keine Wurzel entsprechenden Rangs existiert. Nach dem Entfernen des Knoten x aus der Wurzelliste fügen wir die Kinder eines nach dem anderen in die Wurzelliste ein und aktualisiern in jedem Schritt das array. Soll eine bereits besetzte Position des arrays beschrieben werden, so wird ein Link-Schritt ausgeführt und versucht, einen Pointer auf die neue Wurzel in die nächsthöhere Position im array zu schreiben. Dies zieht evtl. weitere Link-Schritte nach sich. Nach Abschluß dieser Operation enthält die Fibonacci-Heap nur verschiedene Bäume. Liegt der kanonische Fall vor, daß ausschließlich Binomialbäume im Spiel sind, so erhalten wir durch DeleteMin -Operation eine Binomial-Queue.

6.

DecreaseKey($K,\Delta$) :

entferne x;
y=P(x);
füge x unmittelbar in die Wurzelliste ein;
Key(x) := Key(x) - $\Delta$;while (y markiert) do
		 entferne y;
		 füge y unmarkiert in die Wurzelliste ein;
		 if (P(y)=NILL) then exit fi
		 y=P(y);
od
markiere y; 

Bemerkung: Wird mit einem leeren oder gar keinem Fibonacci-Heap gestartet, und werden ausschließlich die aufbauenden Operationen Insert , Merge und FindMin angewendet, so können nur Binomialbäume enstehen. In diesem natürlichen Fall also liegt stets ein Binomialwald vor, der jedoch i.a. nicht aufgeräumt ist. Das heißt, es existieren mehrere Binomialbäume B_i desselben Typs, die nicht paarweise zu B_i+1-Bäumen verschmolzen sind. Dies geschieht erst bei der Operation DeleteMin . Man beachte, daß nur nach einer solchen Operation momentan ein Binomial Heap vorliegt, ansonsten nur ein Binomialwald.