Amortisierte Kostenanalyse für Fibonacci-Heaps

Kostenanalyse für Operation Sequenzen:

i)

Summieren der worst-case-Kosten wäre zu pessimistisch. Der resultierende Wert ist i.a. zu groß.

ii)

average-case:

-

Aufwand für Analyse zu hoch

-

realistische Verteilung für Eingabe?

iii)

amortisierte Kostenanalyse: average-case-Analyse über worst-case-Sequenzen von Operationen.

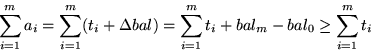
Definition: Wir führen für jede Datenstruktur (Fibonacci-Heap) ein Bankkonto ein und ordnen ihr eine nichtnegative reelle Zahl bal, ihr Potential (bzw. Kontostand) zu. Die amortisierten Kosten für eine Operation ergeben sich als Summe der tatsächlichen Kosten und der Veränderung des Potentials ($\Delta bal$), welche durch die Operation verursacht wird:

t_i:= worst-case-Kosten der i-ten Operation
$\Delta bal_i = bal_i - bal_{i-1}$: Potentialveränderung durch die i-te Operation.
$a_i = t_i + \Delta bal_i$ : ``amortisierte Kosten`` der i-ten Operation
m : Anzahl der Operationen

Falls $bal_m\geq bal_0$ (Was bei bal₀:=0 stets gilt):

$$\sum_{i=1}^{m}{a_i} = \sum_{i=1}^m (t_i + \Delta bal) = \sum_{i=1}^m t_i + bal_m -bal_0 \geq \sum_{i=1}^m t_i$$

Amortisierten Kosten einer Sequenz sind obere Schranke für die tatsächlicher Kosten. Anwendung auf Fibonacci-Heaps:

$$bal:= \char93 \text{ B\uml {a}ume} + 2 \char93 (\text{markierte Knoten $\neq$\space Wurzel})$$

Lemma: Sei x ein Knoten im Fibonacci-Heap mit Rang(x)=k. Seien die Kinder von x sortiert in der Reihenfolge ihres Anfügens an x, dann ist der Rang des i-ten Kindes $\geq i-2$.

Beweis: Zum Zeitpunkt des Einfügens des i-ten Kindes ist der Rang(x) = i-1 (Das i-tes Kind hat zu dieser Zeit auch Rang (i-1)). Danach kann das i-te Kind höchstens einen Sohn verloren haben $\Rightarrow$ Rang $\geq i-2$. $\Diamond$




Beweis: Sei f_k die minimale Anzahl der Elemente im Baum, dessen Wurzel Rang k hat.
$\Rightarrow f_k \geq f_{k-2} + f_{k-3} + \ldots + f_0 + 1 + 1$
Setze: $g_k:=g_{k-2} + g_{k-3} + \ldots + g_0 + 2$, d. h. $f_k \geq g_k$; g₀:=1

$\parbox{110mm}{ \begin{tabular} {llclclclcl} (1) & $g_k$\space & $=... ...row g_k=g_{k-1}+g_{k-2} \Rightarrow f_k \geq g_k = F_{k+2}$}\\ \end{tabular} }$

$\Diamond$

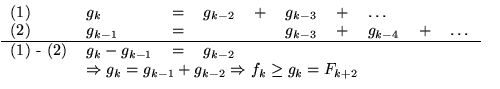
Amortisierte Kosten der FH-Operationen ($a_i = t_i + \Delta bal_i$):

• FindMin : $a=t=\mathcal{O}(1)$.
• Insert : $t=\mathcal{O}(1), \Delta bal= +1 \Rightarrow a=\mathcal{O}(1)$.
• Merge : $t=\mathcal{O}(1), \Delta bal= 0 \Rightarrow a=\mathcal{O}(1)$.
• DeleteMin :
  
  $\left.\begin{array} {l} \text{Einf\uml {u}gen der Kinder von }x \text{ in Wurz... ...indet amortisiert}\\ \end{array}\right\} \Rightarrow a = \mathcal{O}(\log N)$
• DecreaseKey : Es ist $\Delta bal = 3 - (\char93$ kaskadierte Schritte)
  
  $\left.\begin{array} {l} \text{Jeder Schritt erh\uml {o}ht die }\char93 \text{... ...Markierung}\\ bal + = 2\\ \end{array}\right\} \Rightarrow a=\mathcal{O}(1)$

Literatur:
Fredman, Tergen: Fibonacci-Heaps and their uses in improved network optimization algorithmus, Procceedings of the $25^{\text{th.}}$, FOCS, 1984, S. 338-346