



Next: Splay-Trees als Suchbäume
Up: Sich selbst organisierende lineare
Previous: Sich selbst organisierende lineare
- Priority Queue
- Variante von Leftist-Bäumen [s.Knuth]: Ein Leftist-Baum ist ein (interner) binärer
Suchbaum, so daß für jeden der Knoten gilt, daß ein kürzester Weg zu einem Blatt über
das rechte Kind führt.
Wir wollen folgende Operationen unterstützen:
 alle Operationen lassen sich auf
Merge
zurückführen
alle Operationen lassen sich auf
Merge
zurückführen
Operationen:
- 1.
- Insert(T,x)
: neuer Baum mit x als Element, merge diesen mit T
- 2.
- FindMin
:
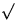 (Minimum an der Wurzel, wegen Heap-Bedingung)
(Minimum an der Wurzel, wegen Heap-Bedingung)
- 3.
- DeleteMin
:
- 4.
- Delete
:
- 5.
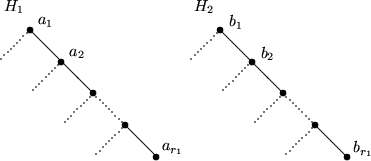
- Merge
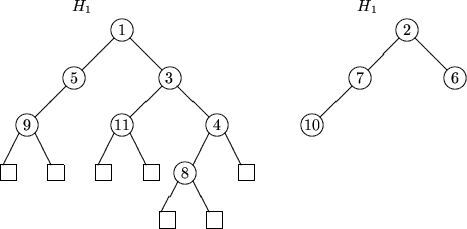
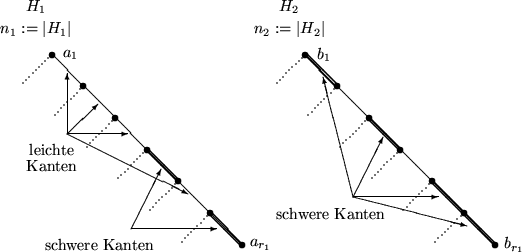
: Seien zwei Heaps H1 und H2 gegeben, seien a1,..,ar1 die Folge der Knoten in H1
von der Wurzel zum rechtesten Blatt,
sei b1,..,br2 die entsprechende Folge in H2.
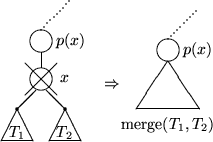
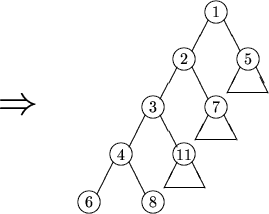
Sei c1,c2,..,cr1+r2 die durch Merging aus (a1,..,ar1) und (b1,..,br2)
entstehende (sortierte) Folge. Mache (c1,..,cr1+r2) zum linkesten Pfad im neuen Baum und
hänge den jeweiligen anderen (d.h. linken) UB ai bzw. bj als rechten UB des
entsprechenden ci an.
Beispiel:
Amortisierte Kostenanalyse der
Merge
-Operation:
Sei w(x): = Gewicht von x = # Knoten im UB von x (einschließlich x)
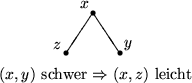
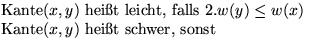
Es gilt: Es ist immer ein Kind über leichte, eins über schwere Kante erreichbar.
Beobachtungen:
- 1.
- (x,y) schwer
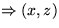 leicht
leicht
- 2.
- Da sich über eine leichte Kante das Gewicht mindestens halbiert, kann ein Pfad von der Wurzel zu einem Blatt
höchstens
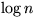 leichte Kanten enthalten.
leichte Kanten enthalten.
Potential: # schwere Kanten zu rechten Kindern
s1:= # schwere Kanten auf den rechten Pfad. s2:= Analog.
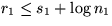
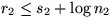
Amortisierte Kosten für
Merge:
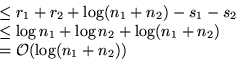
![% latex2html id marker 7976
\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Eine Folge...
...o}\ss{}e des Baumes ist, der in der $i$-ten merge-Operation geschaffen wird.
}}](img336.gif)




Next: Splay-Trees als Suchbäume
Up: Sich selbst organisierende lineare
Previous: Sich selbst organisierende lineare
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
 alle Operationen lassen sich auf
Merge
zurückführen
alle Operationen lassen sich auf
Merge
zurückführen
 alle Operationen lassen sich auf
Merge
zurückführen
alle Operationen lassen sich auf
Merge
zurückführen
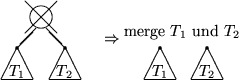
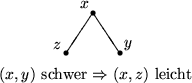
![]()
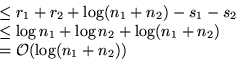
![% latex2html id marker 7976
\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Eine Folge...
...o}\ss{}e des Baumes ist, der in der $i$-ten merge-Operation geschaffen wird.
}}](img336.gif)