



Next: Sich selbst organisierende Binary
Up: Sich selbst organisierende Datenstrukturen
Previous: Motivation
Beim sog. ``Wörterbuchproblem`` ist auf möglichst effiziente Weise eine Menge von bis zu n
Elementen zu organisieren:
- Einfügen
- Löschen
- Reihenfolge ändern
Dabei soll die Effizienz der Implementierung bei beliebigen Sequenzen von m
Operationen untersucht werden. Die Menge wird als unsortierte Liste dargestellt.
Operationen:
- 1.
- Access(i)
: Suchen des Elements i:
Die Liste wird von Anfang an durchsucht, bis das gesuchte Element
gefunden ist. Für das i-te Element betragen die tatsächlichen Kosten i Einheiten.
- 2.
- Insert(i)
: Einfügen des Elements i:
Die Liste wird von Anfang an durchsucht, und wenn sie vollständig durchsucht
wurde und das Element nicht enthalten ist, so wird es hinten angefügt. Diese erfordet
(i+1) Schritte, wenn die Länge der Liste i ist.
- 3.
- Delete(i)
: Löschen des Elements i:
Wie bei
Access
wird die Liste zuerst durchsucht und dann das betreffende Element
gelöscht. Diese kostet im Falle des i-ten Elements i Schritte.
Nach Abschluß einer jeden Operation können gewisse Umordnungsschritte stattfinden,
die spätere Operationen beschleunigen.
Annahme:
Wir nehmen an, daß nach Ausführung jeder
Access
- oder
Insert
-Operation,
die auf Element i angewandt wird, dieses Element kostenlos um beliebig viele
Positionen in Richtung Listenanfang geschoben werden kann. Wir nennen jede daran beteiligte
Elementenvertauschung einen kostenlosen Tausch. Jeder andere Tausch zweier Elemente ist ein
bezahlter Tausch und kostet eine Zeiteinheit.
Ziel:
Es soll eine einfache Regel gefunden werden, durch die mittels obiger Vertauschungen die Liste
so organisiert wird, daß die Gesamtkosten einer Folge von Operationen minimiert werden. Wir
sprechen von ``selbstorganisierenden linearen Listen`` und untersuchen hierzu folgende Regeln:
- MFR (Move-to-Front-Rule):
Access
und
Insert
stellen das betreffende Element vorne
an die Liste an und verändern ansonsten nichts.
- TR (Transposition-Rule):
Access
bringt das Element durch eine
Vertauschung um eine Position nach vorne, insert hängt es ans Ende der Liste
an.
Bemerkung:
- -
- Die MFR erlaubt die Ausführung einer Sequenz von Operationen
Access
,
Insert
und
Delete
mit einer amortisierten Laufzeit, die um höchstens
den konstanten Faktor 2 schlechter ist als ein optimaler Listenalgorithmus.
- -
- Für die TR dagegen gibt es keinen solchen konstanten Faktor. Sie kann verglichen mit
MTR bzw. einem optimalen Algorithmus beliebig schlecht sein.
Für die Algorithmen nehmen wir an:
- 1.
- Kosten für
Access(xi)
und
Delete(xi)
sind gleich der Position
von xi in der Liste (von Anfang an gezählt).
- 2.
- Kosten für
Insert(x)
(x nicht in Liste) ist der Länge der Liste
nach der
Insert
-Operation (d.h. neue Elemente werden zunächst an Listenende)
angehängt
- 3.
- Ein Algorithmus kann die Liste jederzeit umorganisieren (die Reihenfolge ändern).
- (a)
- kostenlose Vertauschung: nach einer
Access(x)
- oder
Insert(x)
-Operation
kann x beliebig näher an den Anfang der Liste verschoben werden.
- (b)
- bezahlte Vertauschung: jede andere Vertauschung benachbarter
Listenelemente kostet eine Einheit.
Bemerkung: MFR (und auch Transpose) benutzen nur kostenlose Vertauschungen.
3a ist pessimistisch für MFR.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $s$\space eine beliebige Folge von...
...t{A}}(s) + \text{X}_{\text{A}}(s) - \text{F}_{\text{A}}(s) - m$
\end{center}}}](img303.gif)
Beweis:
Potentialfunktion: 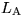 bzw.
bzw. 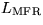 seien die Listen, A
bzw. MFR (führt bei Eingabesequenz s) sind die Algorithmen.
seien die Listen, A
bzw. MFR (führt bei Eingabesequenz s) sind die Algorithmen.
Potential := Anzahl der Inversionen in 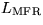 im Vergleich zu
im Vergleich zu 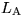
D.h. sei o.B.d.A. 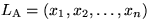 .
.
Dann ist die Potential:
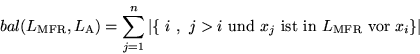
Wir betrachten im folgenden
Insert(x)
als ein
Access
auf ein (fiktives) (n+1)-tes
Element. Eine Operation (
Access(xi)
bzw.
Delete(xi)
) kostet für A dann i
Einheiten und für MFR t Einheiten, wobei t die Position von xi in  ist.
ist.
- i)
- A ändert (bei
Access
bzw.
Delete
)
 in kanonischer Weise.
Für Element xi sind die Kosten i-Einheiten.
in kanonischer Weise.
Für Element xi sind die Kosten i-Einheiten.
- ii)
- Die amortisierten Kosten einer Operation (
Access(xi)
oder
Delete(xi)
)
für MFR sind
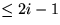
Sei k die Anzahl der Elemente (wie xj), j>i, die im 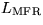 vor xi stehen.
t ist die Position xi im
vor xi stehen.
t ist die Position xi im 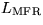 :
:
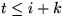 ;
; 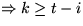
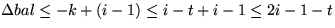 (bei Access)
(bei Access)
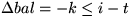 (bei Delete)
Amortisierte Kosten
(bei Delete)
Amortisierte Kosten 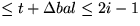 .
.
- iii)
- Die amortisierten Kosten einer kostenlosen Vertauschung durch Algorithmus A sind
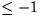
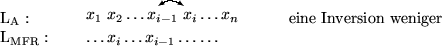
- iv)
- Die amortisierten Kosten einer bezahlten Vertauschung durch Algorithmus A sind
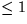
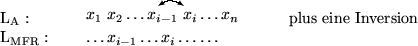
Anfangspotential : 0
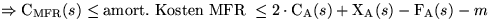

Anmerkung: Wenn wir nicht mit einer leeren Liste (oder zwei identischen
Listen, d.h. L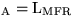 ) starten, ergibt sich:
) starten, ergibt sich:
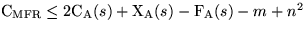
Literatur:
Sleator, D.R., Tarjan: Amortized efficiency of list update and paging rules.
Comm. ACM 28(2), p. 202-208 (1985).




Next: Sich selbst organisierende Binary
Up: Sich selbst organisierende Datenstrukturen
Previous: Motivation
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]()
![]()
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $s$\space eine beliebige Folge von...
...t{A}}(s) + \text{X}_{\text{A}}(s) - \text{F}_{\text{A}}(s) - m$
\end{center}}}](img303.gif)
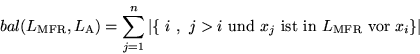
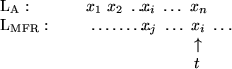
vor xi stehen. t ist die Position xi im
:
;
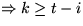
(bei Access)
(bei Delete) Amortisierte Kosten
.