![\begin{picture}
(100,45)(20,2.5)
\put(20,25){
\framebox
(95,5){}}
\put(25,25)...
...(96,11){\vector(1,1){1.5}}
\put(50,4.5){\makebox(35,5)[b]{Delete}}\end{picture}](img440.gif)
![\begin{picture}
(100,46)(20,12.5)
\put(20,25){
\framebox
(95,5){}}
\put(25,25...
...(50,53){\makebox(65,5)[l]{Baum mit $\sqrt{n}$\space Verzweigungen}}\end{picture}](img441.gif)
![\begin{picture}
(100,45)(20,2.5)
\put(20,25){
\framebox
(95,5){}}
\put(25,25)...
...(96,11){\vector(1,1){1.5}}
\put(50,4.5){\makebox(35,5)[b]{Delete}}\end{picture}](img440.gif)
![\begin{picture}
(100,46)(20,12.5)
\put(20,25){
\framebox
(95,5){}}
\put(25,25...
...(50,53){\makebox(65,5)[l]{Baum mit $\sqrt{n}$\space Verzweigungen}}\end{picture}](img441.gif)
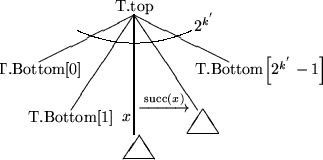
Definition: Eine k-Struktur T für S besteht aus:
- 1.
- der Zahl
- 2.
- einer doppelt verketteten Liste T.list, die die Elemente von S in aufsteigender Reihenfolge enthält
- 3.
- einem Bitvektor
mit
falls
einem Zeiger (Pointer) Vektor
. Falls
, dann zeigt
auf i in der Liste aus 2.
- 4.
- einer k'-Struktur T.top und einem Feld
von k''-Strukturen. Falls m=1, dann T.top, T.bottom und die zugehörigen k''-Strukturen leer,
.
, der Bitvektor wird nicht benötigt. Falls m>1, dann ist T.top eine k'-Struktur für die durch
gegebene Menge, und für jedes
ist
eine k''-Struktur für die Menge
Beispiel:
![]()
![\begin{picture}
(105,46)(0,5)
\put(0,25){\makebox(19,5)[l]{T.p}}
\put(20,25){
...
...5,27.5){\vector(0,-2){10}}
\put(0,12.5){\makebox(15,5)[l]{T.list}}\end{picture}](img461.gif)
if k=1 or
then naive Suche else if
or
then return( Succ(x) gibt's nicht) else
;
; if
and
then return(
+ Succ(
) else z':= Succ(
, return(
) fi fi fi
Insert Operation:
Insert(x',T.top) , Insert(x'',T.bottom[x']) (nur ein nicht trivialer rekursiver Aufruf)
Delete
Operation:
Komplexität von
Delete
in k-Struktur: ![]()
Kosten der Initialisierung: ![]() Größe der Datenstruktur
Größe der Datenstruktur
Platzbedarf für k-Struktur: Sei S(k) der Platzbedarf für eine k-Struktur.
Dann gilt:
S(1)=c
S![]() für
für ![]()
Wir ersetzen zur Vereinfachung:
S![]()
Lemma:
S![]()
Beweis:
Setze: S![]() (besser: Zeige S
(besser: Zeige S![]() funktioniert)
funktioniert)
Für k=1 klar
Rekursionsschritt:
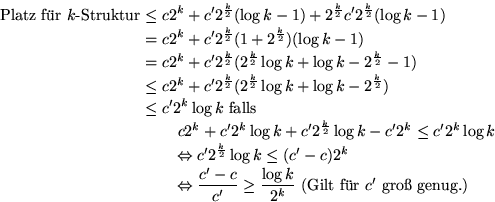
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $N=2^k$, Universum $U=\{0,\ldots,...
...O}(N\log\log N)$. Der Platzbedarf ist ebenfalls
$\mathcal{O}(N\log\log N)$.
}}](img495.gif)