

Invarianten:
Operationen:
for i=0 to B do
od u[0]=0; u[1]=1; for i=2 to B dou[i]:=u[i-1]+2i-2 od
i:=B; while u[i]> Key(x) do i:=i-1 od füge x in b[i] ein;
; entferne x aus b[i]; Key(x) := k; co Überprüfung, das alles stimmt oc while (u[i]>k) do i:=i-1 od füge x in b[i] ein;
Beispiel:i:=0; Entferne und (und gib zurück) ein beliebiges Element in b[i]; if
Elemente in Radix-Heap = 0 then return; while
do i:=i+1; k := kleinster Schlüssel in b[i]; u[0] = k; u[1] = k+1; for j=2 to i do
od od verteile alle Elemente aus b[i] auf
;
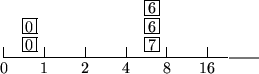
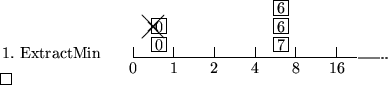
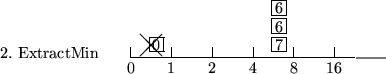
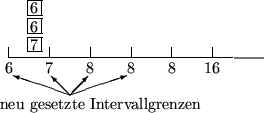
![]() Intervallgröße
Intervallgröße ![]()
Innerhalb b[i] stehen i-1-Buckets zur Verfügung mit Intervallen ![]() bzw.
höchstens u[i+1]. Da alle Schlüsseln in b[i] aus dem Intervall
bzw.
höchstens u[i+1]. Da alle Schlüsseln in b[i] aus dem Intervall ![]() sind, passen sie alle
in
sind, passen sie alle
in ![]() .
.
Analyse der amortisierten Kosten:
![]()
![% latex2html id marker 12514
\fbox {\parbox[c]{11.5cm}{\textbf{Satz:}
Ausgehend...
... Radix-Heap:
\begin{equation*}
\mathcal{O}(k \log{C} +l)
\end{equation*}
}}](img524.gif)