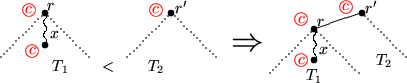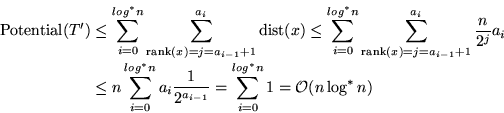Next: Erweiterung
Up: Union-Find-Datenstruktur
Previous: Gewichtete Union (erste Verbesserung)
Problem: Folge von k
Find
- und
Union
-Operationen auf einen Operation mit n
Elementen, darunter n-1
Union
.
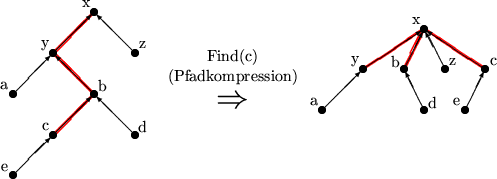
Implementierung: Gewichtete
Union
,
Find
's für Pfad-Kompression:
Bemerkung:
Nach der Definition ist 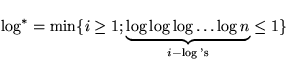 .
.
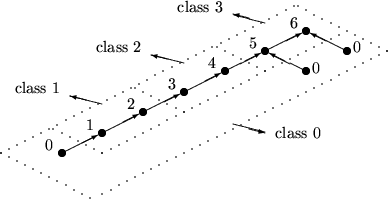
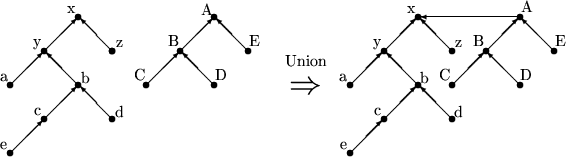
Beispiele:
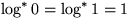
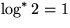
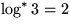
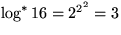
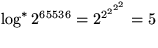
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
In der obigen Situation ergibt sich ei...
...rtisierte Komplexit\uml {a}t
von $\mathcal{O}(\log^*n)$\space pro Operation.
}}](img539.gif)
Beweis:
Sei T' der (endgültige) In-Baum, der durch die Folge der
Union
's, ohne die
Find
's
entstehen würde (also keine Pfad-Kompression). Ordne jedem Element x drei Werte zu:
- rank(x):= Höhe des Unterbaums in T' mit Wurzel x
- class(x):=
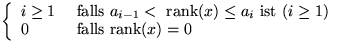
Dabei gilt: 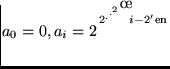 für
für 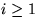
- dist(x) ist die Distanz von x zu einem Vorfahr y im momentanen Union-Find-Baum (mit
Pfad-Kompression) mit class(y) > class(x) bzw. y ist Wurzel des Baumes.
Definiere eine geignete Potentialfunktion:
- Potential :=
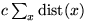 c ist eine geignete Konstante >0
c ist eine geignete Konstante >0
Beobachtungen:
- i)
- Sei T ein Baum in der aktuellen Union-Find-Stuktur (mit Pfad-Kompression), seien x,y
Knoten im T, y Vater von x
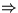 class(
class(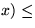 class(y).
class(y).
- ii)
- Aufeinander folgende
Find(x)
besitzen (bis auf eine) verschiedene Kanten. Diese
Kanten sind (im wesentlichen) eine Teilfolge der Kanten in T' auf dem Pfad von x zur Wurzel.
Amotisierte Kosten
Find(x)
:
Sei 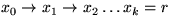 die Pfad von x0 zur Wurzel. Kanten
(xi-1,xi) mit class(xi-1) = class(xi). Es gibt höchstens
die Pfad von x0 zur Wurzel. Kanten
(xi-1,xi) mit class(xi-1) = class(xi). Es gibt höchstens 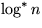 -Kanten
(xi-1,xi) mit class(xi-1) < class(xi). Ist class(xi-1) = class(xi) und i<k
(also
-Kanten
(xi-1,xi) mit class(xi-1) < class(xi). Ist class(xi-1) = class(xi) und i<k
(also 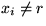 ), dann ist dist(xi-1) vor der
Find(x)
-Operation
), dann ist dist(xi-1) vor der
Find(x)
-Operation 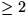 , nachher
gleich 1.
, nachher
gleich 1.
Damit können die Kosten für alle Kanten (xi-1,xi) mit class(xi-1)=class(xi) aus dem
Potentialverringerung bezahlt werden und es ergeben sich amortisierte Kosten:
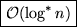
Amortisierte Kosten aller (n-1)-
Union
's zusammen:
Die gesamte Potentialerhöhung durch alle
Union
's ist nach oben durch das Potential von
T' beschränkt (Beobachtung ii).
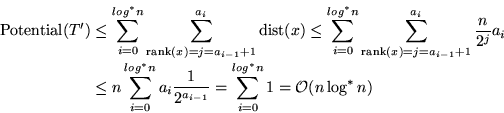





Next: Erweiterung
Up: Union-Find-Datenstruktur
Previous: Gewichtete Union (erste Verbesserung)
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999


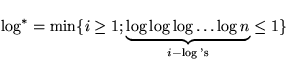 .
. ![]()
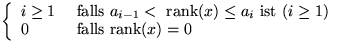
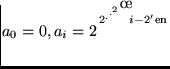 für
für