Erweiterung

1)

Bessere obere Schranke $\alpha(k,n), k\geq n$. Ackermannfunktion: A(m,n):
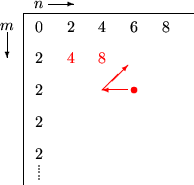
A(0,n) = 2n ; $n\geq0$
A(m,0) = 2 ; $m\geq1$
A(m+1,n+1) := A(m,A(m+1,n))

Die Ackermannfunktion steigt asymptotisch schneller als jede primitiv-rekursive Funktion.

Definition: Die Klasse der primitiv rekursiven Funktionen (auf den natürlichen Zahlen) ist induktiv wie folgt definiert:

1.

Alle konstanten Funktionen sind primitiv rekursiv.

2.

Alle identischen Abbildungen (Projektionen) sind primitiv rekursiv.

3.

Die Nachfolgerfunktion auf den natürlichen Zahlen ist primitiv rekursiv.

4.

Jede Funktion, die durch Einsetzung (Komposition) von primitiv rekursiven Funktionen entsteht, ist selber primitiv rekursiv.

5.

Jede Funktion, die durch sog. primitive Rekursion aus primitiv rekursiven Funktionen entsteht, ist primitiv rekursiv. Primitive Rekursion bedeutet, daß die definition von $f(n+1,\cdots)$ zurückgeführt wird auf $f(n,\cdots)$. Formaler, f muß ein Gleichungssystem der folgenden Form erfüllen:

$$\begin{split} f(0,\cdots) & = g(\cdots)\\ f(n+1,\cdots) & = h(f(n,\cdots),\cdots)\end{split}$$

wobei g,h bereits primitiv rekursive Funktionen sind.

$\alpha(n,n) = \min \{ i; A(i,i) \geq n \}$
Ebenso entsprechend die untere Schranke.

2)

Varianten