



Next: Der Schönhage-Paterson-Pippenger-Median-Algorithmus
Up: Selektieren und Sortieren
Previous: Der Blum-Floyd-Pratt-Rivest-Tarjan Selektions-Algorithmus
Problem: Bestimme den Median von n Elementen:
- 1.
- Wähle
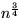 Elemente zufällig aus dem n Elementen aus.
Elemente zufällig aus dem n Elementen aus.
- 2.
- Sortiere diese
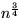 Elemente mit einem
Elemente mit einem 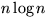 -Algorithmus.
-Algorithmus.
- 3.
- Setze
- p1
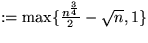 -kleinsten Element der
-kleinsten Element der 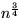 Elemente.
Elemente.
- p2
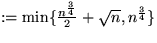 -kleinsten Element der
-kleinsten Element der 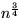 Elemente.
Elemente.
- 4.
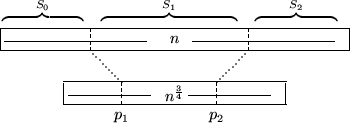
- Partitioniere n Elemente in
- S0
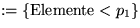
- S1
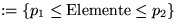
- S2
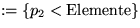
- 5.
- Falls
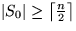 oder
oder 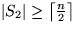 oder
oder 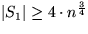 dann wiederhole den
Algorithmus
dann wiederhole den
Algorithmus
ansonsten sortiere S1 und liefer das 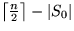 -kleinste
Element davon ab.
-kleinste
Element davon ab.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Obiger Algorithmus bestimmt den Median...
...enten mit einer erwarteten Anzahl
von $\frac{3}{2}n+o(n)$\space Vergleichen.
}}](img599.gif)
Beweis:
- i)
- Korrektheit: klar.
- ii)
- Anzahl der Vergleichen einer Iteration:
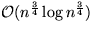 + Kosten der Partitionierung
+ Kosten der Partitionierung
Kosten der Partitionierung: zu naiv, bessere Ansatz:
Wähle zuerst mit der Wahrscheinlichkeit je 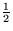 aus, ob Element x mit p1 oder p2
verglichen wird, mache zwei Vergleiche nur, falls nötig. Erwartete Anzahl Vergleiche dafür ist
gleich:
aus, ob Element x mit p1 oder p2
verglichen wird, mache zwei Vergleiche nur, falls nötig. Erwartete Anzahl Vergleiche dafür ist
gleich:
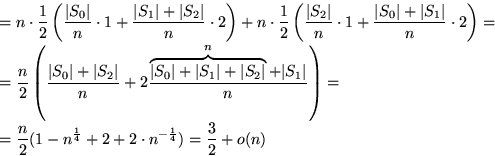
Wir zeigen, daß der Algorithmus mit der Wahrscheinlichkeit 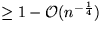 nur
eine Iteration benötigt (daraus folgt, daß insgesamt Anzahl der Vergleiche
nur
eine Iteration benötigt (daraus folgt, daß insgesamt Anzahl der Vergleiche 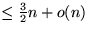 ist). Dafür verwenden wir Hilfsmittel aus der Stochastik:
ist). Dafür verwenden wir Hilfsmittel aus der Stochastik:
Auswahl der 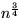 Elemente wird wiederholt, falls
Elemente wird wiederholt, falls 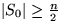 .
Dies passiert gdw. wir höchstens
.
Dies passiert gdw. wir höchstens 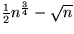 Elemente aus der Hälfte der aller Elemente
Elemente aus der Hälfte der aller Elemente 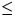 Median auswählen.
Median auswählen.
Was ist also die Wahrscheinlichkeit dafür, daß keine neue Auswahl der 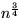 Elemente
stattfinden muß?
Elemente
stattfinden muß?
Setze Binäre Zufallsvariable für jedes 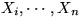 mit:
mit:
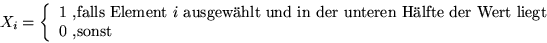
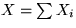 binomialverteilt mit Parametern n und
binomialverteilt mit Parametern n und 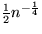
E(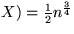 , Var(
, Var(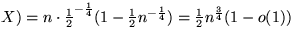
Die Wahrscheinlichkeit hierbei ist:
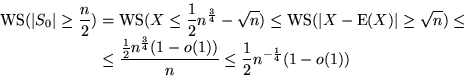
Die Wahrscheinlichkeit für den Fall, daß man von vorne anfangen muß:
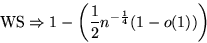
Die anderen beiden Wahrscheinlichkeitsbedingungen (WS(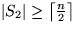 ) und WS(
) und WS(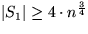 ))
ergeben analoge Abschätzungen
))
ergeben analoge Abschätzungen 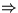 Widerholung mit
WS
Widerholung mit
WS 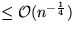





Next: Der Schönhage-Paterson-Pippenger-Median-Algorithmus
Up: Selektieren und Sortieren
Previous: Der Blum-Floyd-Pratt-Rivest-Tarjan Selektions-Algorithmus
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
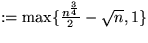 -kleinsten Element der
-kleinsten Element der 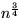 Elemente.
Elemente.
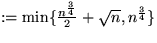 -kleinsten Element der
-kleinsten Element der 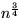 Elemente.
Elemente.
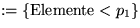
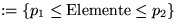
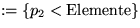

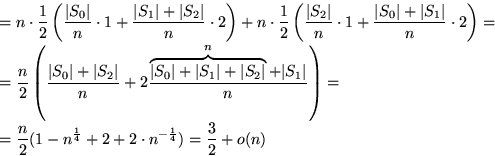
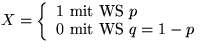
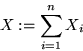
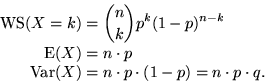
![]()
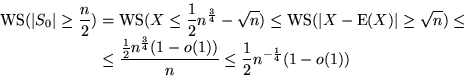
![]()