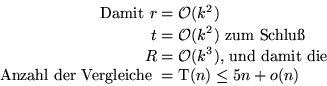Next: Eine untere Schranke für
Up: Selektieren und Sortieren
Previous: Randomisierter-Median-Algorithmus
Definition: Sei 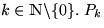 ist die folgende
partielle Ordnung:
ist die folgende
partielle Ordnung:
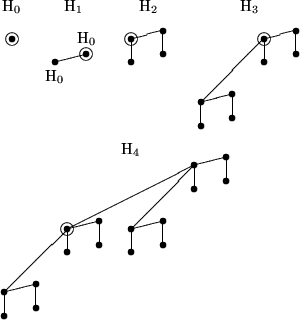
Spezielle Binomialbäume mit ,,Zentren``.
Definition:
- 1.
- Der Baum H0 besteht aus einem Knoten und dieser ist auch das
Zentrum.
- 2.
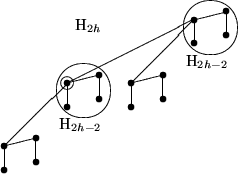
- H2h (h>0) besteht aus zwei H2h-1, deren Zentren durch
eine neue Kante verbunden sind. Das Zentrum des H2h ist das kleinere
der beiden Zentren der H2h-1.
- 3.
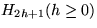 besteht aus zwei H2h, deren Zentren durch
eine neue Kante verbunden sind, sein Zentrum ist das größere dieser
beiden Zentren.
besteht aus zwei H2h, deren Zentren durch
eine neue Kante verbunden sind, sein Zentrum ist das größere dieser
beiden Zentren.
Das Zerlegungslemma:
- a)
- Hh hat 2h Knoten, es werden 2h-1 Vergleiche benötigt, um
Hh zu konstruieren.
- b)
- H2h kann zerlegt werden in
- sein Zentrum
- eine Menge
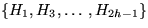 von disjunkten
Teilbäumen, deren Zentren alle größer sind als das Zentrum von
H2h.
von disjunkten
Teilbäumen, deren Zentren alle größer sind als das Zentrum von
H2h.
- eine Menge
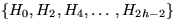 von disjunkten
Teilbäumen mit Zentren kleiner als das von H2h.
von disjunkten
Teilbäumen mit Zentren kleiner als das von H2h.
- c)
- H2k+1 kann so zerlegt werden, daß die Zusammenhangskomponente
des Zentrums genau 2k Knoten
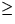 dem Zentrum enthält, indem
höchstens 2k+1-1 Kanten entfernt werden.
dem Zentrum enthält, indem
höchstens 2k+1-1 Kanten entfernt werden.
H2k kann so zerlegt werden, daß die Zusammenhangskomponente des
Zentrums genau 2k Knoten enthält, die alle 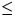 dem Zentrum sind,
indem höchstens 2k-1 Kanten entfernt werden.
dem Zentrum sind,
indem höchstens 2k-1 Kanten entfernt werden.
- d)
- Falls
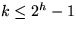 , dann kann H2h so zerlegt werden, daß
die Zusammenhangskomponente des Zentrums genau 2k+1 Elemente enthält,
von denen k größer und k kleiner als das Zentrum sind
(
, dann kann H2h so zerlegt werden, daß
die Zusammenhangskomponente des Zentrums genau 2k+1 Elemente enthält,
von denen k größer und k kleiner als das Zentrum sind
(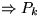 ).
).
Dazu genügt es, höchstens 3k+2h Kanten zu entfernen. Die restlichen
Zusammenhangskomponenten sind wieder Hi.
Bemerkung: Bei jedem Konstruktionsschritt wird ein Vergleich durchgeführt,
um zu bestimmen, welcher der beiden Teilbäume das kleinere Zentrum hat.
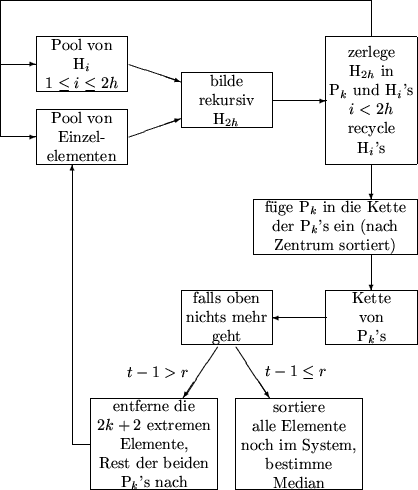
Im Algorithmus von Schönhage, Paterson und Pippenger werden aus
Teilstücken Hr größere Bäume Hr+1 zusammengebaut, wodurch
schrittweise eine partielle Ordnung auf den Eingabewerten bestimmt wird.
Wurde ein Baum H2h hinreichender Größe hergestellt, so wird er durch
Zerlegung in einen Baum umgewandelt, der nur noch sein altes Zentrum,
sowie k darüberliegende und k darunterliegende Elemente
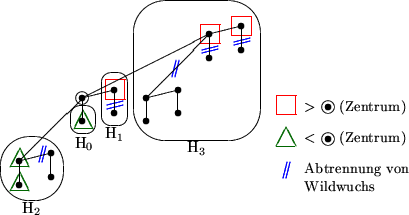
enthält, wobei 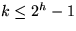 . Im folgenden Beispiel wollen wir H4
zerlegen und wählen k = 3:
. Im folgenden Beispiel wollen wir H4
zerlegen und wählen k = 3:
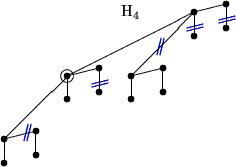
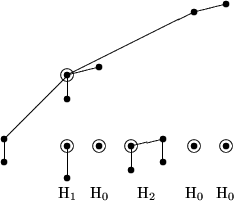
Um einen H4 derart zu zerlegen, müssen wir 5 Kanten aufbrechen.
Dabei werden drei H0, ein H1 sowie ein H2 abgespalten.
Übrig bleibt die gewünschte Struktur mit k Knoten über dem Zentrum
und k unter dem Zentrum, wodurch eine partielle Ordnung auf 2k+1
Eingabewerten bestimmt wurde:
Die bei der Zerlegung angefallenen Reststücke werden beim Aufbau weiterer
Bäume benutzt. So geht das bereits angesammelte Wissen
über die Ordnung der Elemente nicht verloren.
Beweis der Teile a) bis d) des Zerlegungslemmas:
- a)
- Lemma 1: Hr hat 2r Knoten, es werden 2r-1 Vergleiche benötigt, um Hr
aufzubauen.
Beweis: In jedem der r Konstruktionsschritte wird die Anzahl der Knoten
verdoppelt. Da wir mit einem Knoten beginnen, hat Hr folglich 2r Knoten.
Die Anzahl der notwendigen Vergleiche Cr
unterliegt folgender Rekursionsgleichung (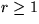 ):
Cr=1+2Cr-1 und C0=0. Damit folgt sofort Cr=2r-1.
):
Cr=1+2Cr-1 und C0=0. Damit folgt sofort Cr=2r-1.

- b)
- Lemma 2: Hr kann in folgende disjunkte Bereiche unterteilt werden:
- sein Zentrum,
- eine Reihe H1, H3, ..., Hr-1 (r gerade) bzw. ..., Hr-2
(r ungerade) von Unterbäumen, deren
Zentren über dem von Hr liegen,
- eine Reihe H0, H2, ..., Hr-2 (r gerade) bzw. ..., Hr-1
(r ungerade) von Unterbäumen, deren Zentren unter dem von Hr liegen.
Beweis: durch Induktion über r. Induktionsanfang: für H0
gilt die Behauptung. Induktionsannahme: die Behauptung gelte für Hr-1.
- 1.
- Sei r = 2h, h > 0.
H2h besteht aus zwei H2h-1, wobei das kleinere
der beiden alten Zentren das neue Zentrum z bildet. Wende auf den H2h-1,
der z enthält, die Induktionsannahme an. Wir können
diesen Unterbaum also in z, sowie H1, H3, ..., H2h-3
(Zentren über z) und
H0, H2, ..., H2h-2 (Zentren unter z) partitionieren.
Zusammen mit dem H2h-1, dessen Zentrum über z liegt, ergibt sich die
Induktionsbehauptung für H2h.
- 2.
- Sei
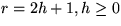 . H2h+1 besteht aus zwei H2h, wobei das
größere der beiden alten Zentren das neue Zentrum z bildet.
Wende auf den H2h, der z enthält, die Induktionsannahme an.
Wir können diesen Unterbaum also in z,
sowie H1, H3, ..., H2h-1 (Zentren über z)
und H0, H2, ..., H2h-2 (Zentren unter z) partitionieren.
Zusammen mit dem H2h, dessen Zentrum unter z liegt, ergibt sich die
Induktionsbehauptung für H2h+1.
. H2h+1 besteht aus zwei H2h, wobei das
größere der beiden alten Zentren das neue Zentrum z bildet.
Wende auf den H2h, der z enthält, die Induktionsannahme an.
Wir können diesen Unterbaum also in z,
sowie H1, H3, ..., H2h-1 (Zentren über z)
und H0, H2, ..., H2h-2 (Zentren unter z) partitionieren.
Zusammen mit dem H2h, dessen Zentrum unter z liegt, ergibt sich die
Induktionsbehauptung für H2h+1.

Wir bezeichnen im folgenden mit H2h- den Baum, der entsteht, wenn wir
H2h so zerlegen, daß alle Elemente oberhalb des Zentrums wegfallen.
Mit H2h+1+ bezeichnen wir den Baum, der entsteht, wenn wir
H2h+1 so zerlegen, daß alle Elemente unterhalb des Zentrums wegfallen.
- c)
- Lemma 3: H2h- und H2h+1+ haben jeweils 2h Knoten. Bei der
Herstellung aus H2h bzw. H2h+1 werden
2h-1 bzw. 2h+1-1 Kanten aufgebrochen. Die wegfallenden Teile
haben die Form Hs, s < 2h bzw. s < 2h+1.
Beweis: Durch Induktion über r. Induktionsanfang: für H0 und H1
gilt die Behauptung. Induktionsannahme: die Behauptung gilt für
alle Hp, p < r.
- 1.
- Sei r = 2h, h > 0. Wir betrachten die Partitionierung von H2h
mit Zentrum z wie in Lemma 2.
Die Unterbäume H1, H3, ..., H2h-1 haben ihre Zentren
oberhalb von z. Wir trennen sie von H2h, indem wir
h Kanten aufbrechen. Die abgetrennten Teile haben offensichtlich die Form
Hs, s < 2h. Bei den Unterbäumen H0, H2, ..., H2h-2,
mit Zentren unterhalb von z, wenden wir jeweils die Induktionsannahme an,
d.h. wir erzeugen H0-, H2-, ..., H2h-2-. Als Ergebnis
erhalten wir H2h-. Damit gilt für die Zahl der aufzubrechenden Kanten
K-(2h) zur Herstellung von H2h-:
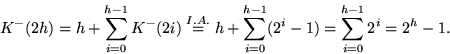
Für die Zahl E-(2h) der Elemente in H2h- gilt:
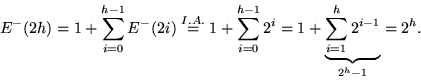
- 2.
- Sei r = 2h+1, h > 0. Wir betrachten die Partitionierung von H2h+1
mit Zentrum z wie in Lemma 2.
Die Unterbäume H0, H2, ..., H2h haben ihre Zentren unterhalb
von z. Wir trennen sie von H2h+1, indem wir h+1 Kanten
aufbrechen. Die abgetrennten Teile haben offensichtlich die Form
Hs, s < 2h+1. Bei den Unterbäumen H1, H3, ..., H2h-1,
mit Zentren oberhalb von z, wenden wir jeweils die Induktionsannahme an,
d.h. wir erzeugen H1+, H3+, ..., H2h-1+. Als Ergebnis
erhalten wir H2h+1+. Damit gilt für die Zahl der aufzubrechenden Kanten
K+(2h+1) zur Herstellung von H2h+1+:
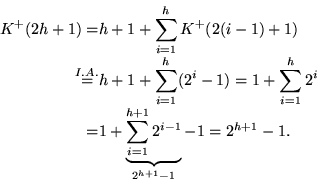
Für die Zahl E+(2h+1) der Elemente in H2h+1+ gilt:
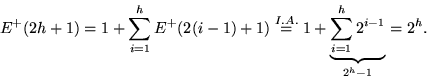

- d)
- Lemma 4: Falls
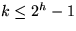 , dann kann H2h so
zerlegt werden, daß die Komponente des Zentrums genau 2k+1 Elemente
enthält, k davon über und k unter dem Zentrum. Dazu müssen
, dann kann H2h so
zerlegt werden, daß die Komponente des Zentrums genau 2k+1 Elemente
enthält, k davon über und k unter dem Zentrum. Dazu müssen
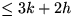 Kanten entfernt werden. Die entfernten Teile sind von der
Form Hs, s < 2h.
Kanten entfernt werden. Die entfernten Teile sind von der
Form Hs, s < 2h.
Beweis: Betrachte die Binärdarstellung von k = k0 20 + k1 21
+ ... + kh-1 2h-1 und die Partitionierung von H2h mit Zentrum
z wie in Lemma 2.
- Für jedes i mit ki = 1, betrachte H2i+1
aus der Sequenz H1, H3, ..., H2h-1 von
Unterbäumen deren Zentren oberhalb von z liegen und schneide alle Elemente
aus H2i+1, die kleiner als sein Zentrum sind (bilde also H2i+1+).
Dazu müssen höchstens 2k Kanten aufgebrochen werden, denn jedes ki = 1
steht für 2i in k, kostet uns aber nach Lemma 2
K+(2i+1) = 2i+1-1 Kanten, also:
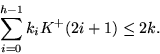
Für jedes i mit ki = 0, schneide H2i+1 ganz weg. Dabei werden
höchstens h Kanten aufgebrochen.
Genau k Elemente oberhalb von z bleiben zurück, da jedes ki = 1 für
2i in k steht, und ein H2i+1+ genau E+(2i+1) = 2i
Elemente enthält, also:
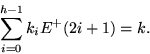
- Für jedes i mit ki = 1, betrachte H2i
aus der Sequenz H0, H2, ..., H2h-2 von
Unterbäumen, deren Zentren unterhalb von z liegen und schneide
alle Elemente aus H2i, die größer als sein Zentrum sind (bilde also
H2i-).
Dazu müssen höchstens k-1 Kanten aufgebrochen werden,
denn jedes ki = 1 steht für 2i in k und kostet uns nach Lemma
3 K-(2i) = 2i-1 Kanten, also:
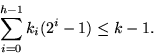
Für jedes i mit ki = 0, schneide H2i ganz weg. Dabei werden
höchstens h Kanten aufgebrochen.
Genau k Elemente unterhalb von z bleiben zurück, da jedes ki = 1 für
2i in k steht, und ein H2i- genau E-(2i) = 2i
Elemente enthält, also:
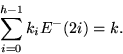
Damit ergibt sich für die Gesamtanzahl aufzubrechender Kanten eine obere
Schranke von 3k+2h. Lemma 3 liefert uns darüberhinaus
die gewünschte Aussage über die Form der abgetrennten Teile.

Betrachte H2h
- ,,größer``:
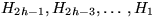
- ,,kleiner``:
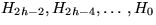
U(h):= Anzahl der Elemente in 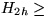 Zentrum:
U(h)=2U(h-1)=2hU(0)=2h
Zentrum:
U(h)=2U(h-1)=2hU(0)=2h
D(h):= Anzahl der Elemente in 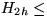 Zentrum:
D(h)=2D(h-1)=2hD(0)=2h
Zentrum:
D(h)=2D(h-1)=2hD(0)=2h
Anzahl der Kanten, die entfernt werden müssen:
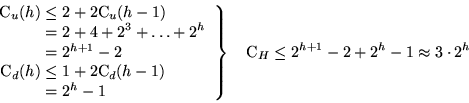
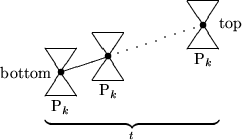
Kette von Pk's:
Gesamtzahl der Elemente:
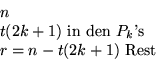
Wenn r<t-1, dann wissen wir, daß top größer ist als
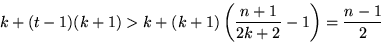
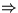 top > Median
top > Median
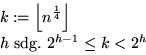
Definiere: r:= Anzahl der noch im H2h Produktionsprozeß steckenden Elemente.
(für jedes i<2h höchstens ein 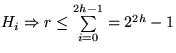 )
)
R:= Anzahl der im letzten Schritt zu sortierenden Elemente. Es gilt: 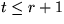 , und damit
, und damit
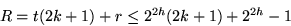
m:= Gesamtzahl der im Algorithmus produzierten Pk's.
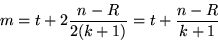
Gesamtzahl der vom Algorithmus durchgeführten Vergleiche =
- 1.
- Anzahl der Kanten in allen Pk's
- 2.
- + Anzahl der Kanten, die gelöscht werden, um die Pk's zu formen
- 3.
- + Anzahl der Kanten, die zum Schluß in übriggebliebenen
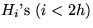 stecken
stecken
- 4.
- + Anzahl der Vergleiche, um jedes Zentrum der Pk's in die (sortierte) Kette einzufügen
- 5.
- + Anzahl der Vergleiche, um die zum Schluß übriggebliebenenen R Elemente zu sortieren
![\begin{displaymath}
\leq \left( \frac{n-R}{k+1}+t \right) \left[ \underbrace{2k}...
...c{n}{2k+1}}_4 \right] + \underbrace{R\log R}_5+\underbrace{r}_3\end{displaymath}](img668.gif)
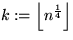 , h so daß
, h so daß 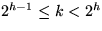
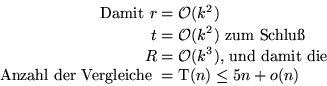
Verbesserte Version: T(n) = 3n + o(n)
Dor/Zwick: 2,95n + o(n)
Bester bekannter Algorithmus: K.Zwick ( 2.95n+o(n) )
Literatur: SPP: Finding the Median. JCSS 13(1976) p.84-199




Next: Eine untere Schranke für
Up: Selektieren und Sortieren
Previous: Randomisierter-Median-Algorithmus
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
ist die folgende partielle Ordnung:
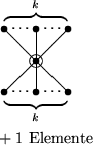
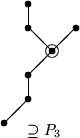
besteht aus zwei H2h, deren Zentren durch eine neue Kante verbunden sind, sein Zentrum ist das größere dieser beiden Zentren.
![]() . Im folgenden Beispiel wollen wir H4
zerlegen und wählen k = 3:
. Im folgenden Beispiel wollen wir H4
zerlegen und wählen k = 3:

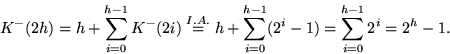
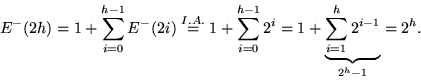
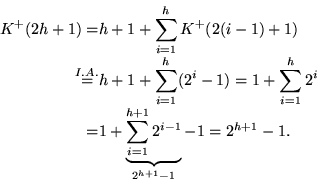
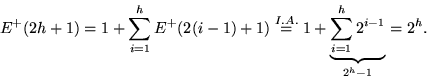
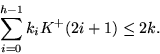
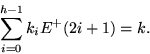
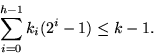
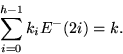
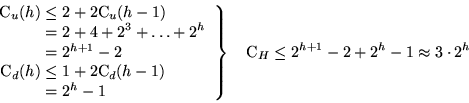
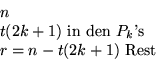
![]()
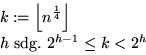
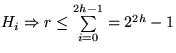 )
)
![]()
![]()
![\begin{displaymath}
\leq \left( \frac{n-R}{k+1}+t \right) \left[ \underbrace{2k}...
...c{n}{2k+1}}_4 \right] + \underbrace{R\log R}_5+\underbrace{r}_3\end{displaymath}](img668.gif)