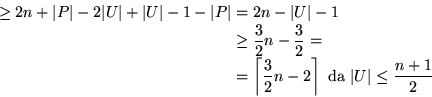Next: Eine bessere untere Schranke
Up: Selektieren und Sortieren
Previous: Der Schönhage-Paterson-Pippenger-Median-Algorithmus
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Jeder (vergleichsbasierte) Medianalgor...
...case
mindestens $\left\lceil \frac{3n}{2} \right\rceil -2$\space Vergleiche
}}](img672.gif)
Beweis: Gegenspielerargument (adversary argument)
n Elemente, o.B.d.A. n ungerade, alle Elemente paarweise verschieden.
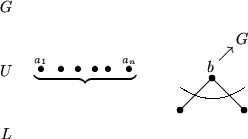
Die Menge aller Elemente wird in drei Teilmengen
partitioniert: U enthält die Kandidaten für den Median, G
enthält Elemente, die sicher größer als der Median sind und
L enthält Elemente, die sicher kleiner als der Median sind.
Anfangs sind alle Elemente in U.
Der Algorithmus stellt nun Fragen der Form ai < aj. Der Gegenspieler
gibt konsistente Antworten, die den Algorithmus jedoch dazu zwingen,
möglichst viele Fragen zu stellen bevor die Antwort feststellen kann(d.h. U soll möglichst
ungeordnet bleiben). Durch die (konsisten!) Antworten des Gegenspielers auf die ``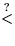 ``-Queries des
Algorithmus entsteht ein DAG. Gegenspieler hält DAG ``einfach``.
``-Queries des
Algorithmus entsteht ein DAG. Gegenspieler hält DAG ``einfach``.
(Angenommen 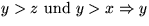 soll sehr groß
sein
soll sehr groß
sein 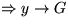 )
)
![\begin{picture}
(97,45)
\put(0,0){\makebox(10,5){$L$}}
\put(0,15){\makebox(1...
...,15){\makebox(5,5)[l]{$a_i$}}
\put(92,25){\makebox(5,5)[l]{$a_j$}}\end{picture}](img676.gif)
![\begin{picture}
(150,45)
\put(0,0){\makebox(10,5){$L$}}
\put(0,15){\makebox(1...
...ut(15,35){\makebox(30,10)[tl]{$\displaystyle \leq\frac{n+1}{2}-1$}}\end{picture}](img678.gif)
Solange 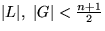 , kann der Algorithmus annehmen,
daß der Median in U ist. Solange U mindestens zwei
unverglichene Elemente und keine Zusammenhangskomponente mit >2
Elementen enthält,
kann der Algorithmus den Median nicht bestimmen.
, kann der Algorithmus annehmen,
daß der Median in U ist. Solange U mindestens zwei
unverglichene Elemente und keine Zusammenhangskomponente mit >2
Elementen enthält,
kann der Algorithmus den Median nicht bestimmen.
Strategie des Gegenspielers: Zwei Phasen
Erste Phase: Query sei 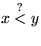 :
:
- i)
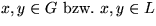 : irgendeine konsistente Antwort
: irgendeine konsistente Antwort
- ii)
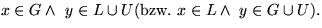 Antwort: y<x (bzw. x<y).
Antwort: y<x (bzw. x<y).
- iii)
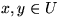
Die erste Phase endet, wenn 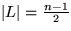 oder
oder 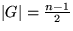 .Während der Phase 1 enthält U mindestens zwei (in U) maximale und mindestens zwei
(in U) minimale Elemente (bzgl. des DAGs).
.Während der Phase 1 enthält U mindestens zwei (in U) maximale und mindestens zwei
(in U) minimale Elemente (bzgl. des DAGs).
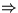 Während Phase 1 kann der Algorithmus den Median mit Sicherheit nicht bestimmen.
Während Phase 1 kann der Algorithmus den Median mit Sicherheit nicht bestimmen.
Der Gegenspieler beginnt mit Phase 2:
|L| wird 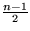 oder |G| wird
oder |G| wird 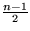
o.B.d.A.:
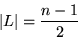
Der Gegenspieler zwingt nun den Algorithmus, das minimale Element in U bzgl. der gesamten totalen Ordnung zu
bestimmen (da dieses unter den Vorgaben der Median ist).
Analyse:
C:= Anzahl der Vergleiche
P:= Anzahl der Paare in U
- i)
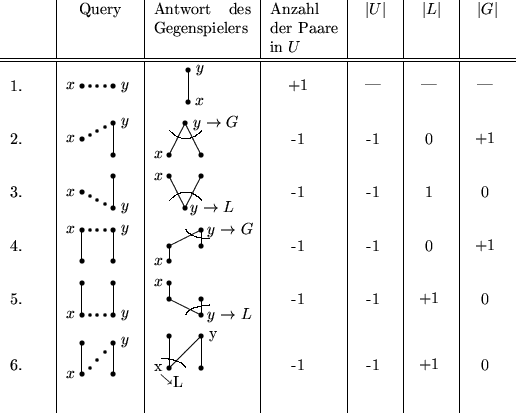
- In der Phase 1 gilt folgende Invariante:
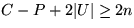
Beweis: vollständige Induktion:
Induktionsanfang: 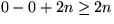
Induktionsschritt: Gemäß der Tabelle.

- ii)
- Sei C
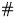 der Vergleiche am Ende der Phase 1, U die am Ende der Phase 2:
In der Phase 2 werden noch
der Vergleiche am Ende der Phase 1, U die am Ende der Phase 2:
In der Phase 2 werden noch 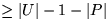 Vergleiche nötig. Die Anzahl der Vergleiche
für alle Phasen:
Vergleiche nötig. Die Anzahl der Vergleiche
für alle Phasen:
Anzahl der Vergleiche 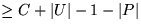 .
.
Am Ende der Phase 1 gilt ja 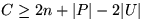 (wg. Invariante).
(wg. Invariante).
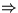 Anzahl der Vergleiche:
Anzahl der Vergleiche:
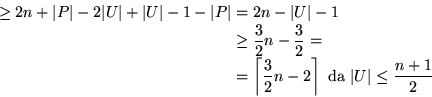





Next: Eine bessere untere Schranke
Up: Selektieren und Sortieren
Previous: Der Schönhage-Paterson-Pippenger-Median-Algorithmus
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![\begin{picture}
(97,45)
\put(0,0){\makebox(10,5){$L$}}
\put(0,15){\makebox(1...
...,15){\makebox(5,5)[l]{$a_i$}}
\put(92,25){\makebox(5,5)[l]{$a_j$}}\end{picture}](img676.gif)

![\begin{picture}
(150,45)
\put(0,0){\makebox(10,5){$L$}}
\put(0,15){\makebox(1...
...ut(15,35){\makebox(30,10)[tl]{$\displaystyle \leq\frac{n+1}{2}-1$}}\end{picture}](img678.gif)