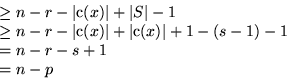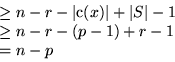Next: Untere Schranke für (vergleichbasiertes)
Up: Selektieren und Sortieren
Previous: Eine untere Schranke für
Literatur: Samuel W. Bent, John W. John: ``Finding the median requires 2n comparisons.''
Proceedings of the 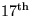 Annual ACM Symposium on Theory of Computing 1985,
p.213-216.
Annual ACM Symposium on Theory of Computing 1985,
p.213-216.
![% latex2html id marker 16025
\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $T$\s...
... \left[\binom{n}{i}\frac{2^{n-p}}{n-i+1}\right]\\ \end{split}\end{equation*}}}](img696.gif)
Bemerkung: 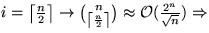 Höhe
Höhe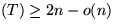 (untere Schranke für Median).
(untere Schranke für Median).
Beweis: Gegenspielerargument + Abzählargument:
,,T hat viele Blätter``, A Teilmenge der Schlüssel, |A|=i;
TA Teilbaum von T, alle Blätter von TA sind auch Blätter von T.
Zu zeigen: TA hat viele Blätter. (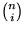 Möglichkeiten, TA's zu
konstruieren, Anzahl Blätter in TA: 2n-p, jedes Blatt von T kommt in höchstens n-i+1
TA's vor)
Möglichkeiten, TA's zu
konstruieren, Anzahl Blätter in TA: 2n-p, jedes Blatt von T kommt in höchstens n-i+1
TA's vor)
Beobachtungen: Jedes Blatt w von T liefert folgende Informationen:
Wähle A als beliebige Teilmenge der n gegebenen Schlüssel, mit |A|=i. Wir
geben für den Gegenspieler eine Strategie an, welche dazu führt, daß wir durch
Zurechtschneiden aus T einen Baum TA konstruieren können, so daß gilt:
- TA ist Binärbaum
- jedes Blatt von TA ist auch Blatt von T (keine zus. Blätter durch Abschneiden)
- für jedes Blatt w von TA gilt:
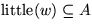
Setze 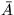 das Komplement von A,
das Komplement von A,
![\begin{displaymath}
\begin{split}
r:=&\ \sqrt{\log\left[\binom{n}{i}\frac{1}{n-i+1}\right]+3}\\ s:=&\ r-1\\ \end{split}\end{displaymath}](img709.gif)
Es gilt: p=r+s-1
Die Konstruktion (das ``Zurechtstutzen``) von T erfolgt in zwei Phasen:
Erste Phase von der Wurzel nach unten (Breitensuche)
Betrachte Knoten x. Definiere:
- C(x) sind die Elemente
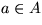 für die es kein
für die es kein 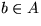 gibt und einen Knoten
auf dem Pfad von der Wurzel von T zu x, an dem kein Vergleich mit einem anderen Element
gibt und einen Knoten
auf dem Pfad von der Wurzel von T zu x, an dem kein Vergleich mit einem anderen Element 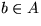 erfolgt ist mit
dem Ergebnis a<b.
erfolgt ist mit
dem Ergebnis a<b.
- c(x) sind entsprechend die in x bekannten Minima in
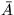 .
. - s(x,a)
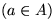 ist die Anzahl der Elemente
ist die Anzahl der Elemente 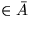 (genauer:
(genauer: 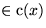 ) mit denen a auf dem Pfad von Wurzel von x verglichen wurde.
) mit denen a auf dem Pfad von Wurzel von x verglichen wurde.
Regeln für Phase 1:
Es werden in Knoten x die Elemente a und b verglichen:
Regel 1.1:
Falls 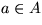 und
und 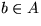 behalte x in TA bei.
behalte x in TA bei.
Regel 1.2: Falls 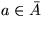 und
und 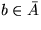 behalte x in TA bei.
behalte x in TA bei.
Regel 1.3:
Sei o.B.d.A. 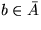 ,
, 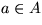 . Ersetze den Unterbaum in T mit
Wurzel x mit dem Unterbaum, dessen Wurzel das Kind von x ist, das dem
Ergebnis entspricht (d.h. lasse den Vergleich a < b aus, nach Voraussetzung
. Ersetze den Unterbaum in T mit
Wurzel x mit dem Unterbaum, dessen Wurzel das Kind von x ist, das dem
Ergebnis entspricht (d.h. lasse den Vergleich a < b aus, nach Voraussetzung
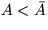 ).
).
Phase 1 läuft solange 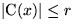 . Ein Knoten auf einem Pfad in T von der
Wurzel, bei dem
. Ein Knoten auf einem Pfad in T von der
Wurzel, bei dem 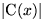 erstmals =r wird, heißt kritisch.Jeder Pfad
in T von der Wurzel zu einem Blatt enthält genau einen kritischen Knoten.
erstmals =r wird, heißt kritisch.Jeder Pfad
in T von der Wurzel zu einem Blatt enthält genau einen kritischen Knoten.
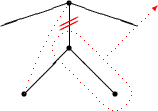
Betrachte in TA einen Pfad von der Wurzel zu einem kritischen Knoten x.
Sei y ein Knoten auf diesem Pfad, z sein Kind.
![\begin{picture}
(26,50)
\multiput(2,2.5)(0,2){23}{\line(0,1){1}}
\multiput(2,2...
...\ \text{C}(z)+\text{c}(z)$}}
\put(4,45){\makebox(20,5)[l]{Wurzel}}\end{picture}](img722.gif)
Dann gilt:
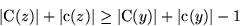
Da 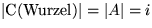 und
und 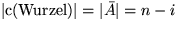 , müssen überhalb
eines jeden kritischen Knoten x mindestens
, müssen überhalb
eines jeden kritischen Knoten x mindestens
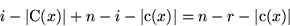
Vergleiche erfolgen. Von jedem kritischen Knoten abwärts arbeitet der
Gegenspieler nach einer Strategie für Phase zwei. Sei x ein solcher
kritischer Knoten. Dann ist 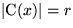 .
.
Phase 2: Sei 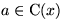 ein Element mit minimalem
ein Element mit minimalem 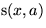 .
.
![\begin{picture}
(104,60)
\put(35,12.5){\oval(70,25)}
\put(72,10){\makebox(5,5)...
...ack[l]{\char93 $\odot=\text{s}(x,a)$\\ f''ur $a\in A$\space fest}}}\end{picture}](img730.gif)
-
- Fall 1:
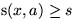 .
.
Betrachte irgendeinen Pfad von der Wurzel
durch x zu einem Blatt w. Jeder solche Pfad muß mindestens n-1
Vergleiche enthalten, um answer(w) zu verifizieren: 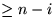 , für
die answer(w) sich (direkt oder indirekt) als das kleinere Element
ergibt, und
, für
die answer(w) sich (direkt oder indirekt) als das kleinere Element
ergibt, und 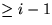 , wo es sich als das größere ergibt.
, wo es sich als das größere ergibt.
Damit sind 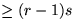 Vergleiche redundant (nämlich alle die, die
zwischen Elementen aus C
Vergleiche redundant (nämlich alle die, die
zwischen Elementen aus C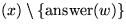 und Elementen
in
und Elementen
in 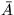 erfolgt sind).
erfolgt sind).
Also:
![\begin{displaymath}
\begin{split}
\text{Tiefe}(T) &\geq n-1+s(r-1)\\ &= n-r-s-...
...g{\left[\binom{n}{i}\frac{2^{n-p}}{n-i+1}\right]}
\end{split} \end{displaymath}](img736.gif)
In diesem Fall folgt also die Behauptung direkt!
-
- Fall 2: s(x,a)<s
-
- Fall 2.1:
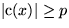 . Sei
. Sei 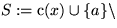 Elemente, die
in s(x,a) gezählt werden. Der Gegenspieler antwortet nun so, daß
das Ergebnis das kleinste Element in S wird. Ist w ein Blatt in TA unter x,
so ist little(w)=
Elemente, die
in s(x,a) gezählt werden. Der Gegenspieler antwortet nun so, daß
das Ergebnis das kleinste Element in S wird. Ist w ein Blatt in TA unter x,
so ist little(w)= 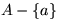
Der Entscheidungsbaum T wird also gemäß folgender Regeln gestutzt
(sei y der aktuelle Knoten und seien a und b die beiden Elemente,
die in y verglichen werden):
-
- Regel 2.1: falls
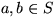 , dann bleibt y erhalten.
, dann bleibt y erhalten.
-
- Regel 2.2: andernfalls, sei oBdA.
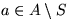 oder
oder 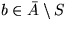 ; ersetze y mit seinem Unterbaum
durch das Kind von y und dessen Unterbaum, das der Antwort von
a<b entspricht.
; ersetze y mit seinem Unterbaum
durch das Kind von y und dessen Unterbaum, das der Antwort von
a<b entspricht.
Also, da überhalb des kritischen Knoten x keine zwei Elemente in
S verglichen wurden, muß der Unterbaum von TA unterhalb von x
Tiefe 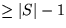 haben.
haben.
Zusammen mit Phase 1 ergibt sich eine Tiefe von TA:
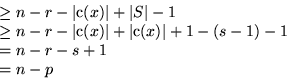
-
- Fall 2.2:
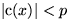 .
. 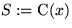
Regeln so, daß der Algorithmus als Antwort das Maximum von S
bestimmt. Tiefe von TA:
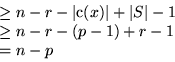
In Wirklichkeit: Jeder Pfad in TA von x zu Blatt hat mindestens die Länge n-p.
Also enthält jedes TA mindestens 2n-p Blätter (von T). Alle TA's
zusammen enthalten 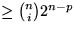 Blätter von T, wobei jedes
Blatt von T höchstens n-i+1 mal vorkommt: Sei w Blatt von T, dann ist
Blätter von T, wobei jedes
Blatt von T höchstens n-i+1 mal vorkommt: Sei w Blatt von T, dann ist
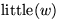 eindeutig bestimmt und muß, falls TA w auch enthält,
little(
eindeutig bestimmt und muß, falls TA w auch enthält,
little(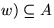 sein. Für das Element in A- little(w) gibt es
sein. Für das Element in A- little(w) gibt es 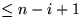 Möglichkeiten
Möglichkeiten
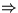 Anzahl Blätter von
Anzahl Blätter von 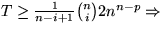 Tiefe
Tiefe![$(T)\geq \log \left[ \binom{n}{i} \frac{2^{n-p}}{n-i+1} \right]$](img753.gif) .
.

Einige Referenzen:
- 1.
- L. Hyafil: Bounds for selection. SIAM J.Compute 5(1976), p.109-114.
- 2.
- S. Beut and John W. John: Finding median requires 2n compression. Proc 17. STOC (1985),
p.213-216.
- 3.
- John Welliaveetil John: A new lower bound for the set-partitioning problem. SIAM J. Compute
17 (1988), p. 640-647.
- 4.
- Doris Dor and Uri Zwick: Median selection requires
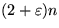 compression. Proc 37
FOCS (1996), p. 125-134
compression. Proc 37
FOCS (1996), p. 125-134
- 5.
- Doris Dor and Uri Zwick: Selecting the median Proc 6 SODA (1995), p. 28-37




Next: Untere Schranke für (vergleichbasiertes)
Up: Selektieren und Sortieren
Previous: Eine untere Schranke für
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![% latex2html id marker 16025
\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei $T$\s...
... \left[\binom{n}{i}\frac{2^{n-p}}{n-i+1}\right]\\ \end{split}\end{equation*}}}](img696.gif)
![\begin{displaymath}
\begin{split}
r:=&\ \sqrt{\log\left[\binom{n}{i}\frac{1}{n-i+1}\right]+3}\\ s:=&\ r-1\\ \end{split}\end{displaymath}](img709.gif)
![\begin{picture}
(115,65)
\put(55,12.5){\oval(60,25)}
\put(55,15){\oval(50,10)}...
...x_i \stackrel{?}{<} y_i$}}
\put(4,52.5){\makebox(20,5)[l]{Wurzel}}\end{picture}](img711.gif)
![\begin{picture}
(26,50)
\multiput(2,2.5)(0,2){23}{\line(0,1){1}}
\multiput(2,2...
...\ \text{C}(z)+\text{c}(z)$}}
\put(4,45){\makebox(20,5)[l]{Wurzel}}\end{picture}](img722.gif)
![]()
![]()
![\begin{picture}
(104,60)
\put(35,12.5){\oval(70,25)}
\put(72,10){\makebox(5,5)...
...ack[l]{\char93 $\odot=\text{s}(x,a)$\\ f''ur $a\in A$\space fest}}}\end{picture}](img730.gif)
![\begin{displaymath}
\begin{split}
\text{Tiefe}(T) &\geq n-1+s(r-1)\\ &= n-r-s-...
...g{\left[\binom{n}{i}\frac{2^{n-p}}{n-i+1}\right]}
\end{split} \end{displaymath}](img736.gif)
![\begin{picture}
(102,60)
\put(35,12.5){\oval(70,25)}
\put(73,10){\makebox(5,5)...
...7.5,37)
\put(57.5,27.5){\makebox(5,5)[tl]{$S$}}
\color {black}
\end{picture}](img737.gif)