Next: Prim's Algorithmus, erste Variante
Up: Grundlagen
Previous: Generischer minimaler Spannbaum-Algorithmus
algorithm Kruskal (G,w):=
 sortiere die Kanten nach aufsteigendem Gewicht in eine Liste L;
initialisiere
sortiere die Kanten nach aufsteigendem Gewicht in eine Liste L;
initialisiere  Wald (n=|V|) mit
Wald (n=|V|) mit  co G=(V,E),
co G=(V,E), 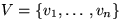 oc
co implementiere Ti's als in-Trees mit den jeweiligen Wurzeln als
Repräsentanten; allgemein: Unio-Find-Problem oc
MSB:=
oc
co implementiere Ti's als in-Trees mit den jeweiligen Wurzeln als
Repräsentanten; allgemein: Unio-Find-Problem oc
MSB:= ; for i:=1 to length(L) do
; for i:=1 to length(L) do
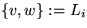 ; x:= Baum
; x:= Baum 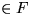 , der v enthält; co x:= Find(v) oc
y:= Baum
, der v enthält; co x:= Find(v) oc
y:= Baum 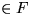 , der w enthält; co y:= Find(w) oc
if
, der w enthält; co y:= Find(w) oc
if 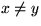 then
co v und w in verschiedenen Bäumen oc
MSB:=MSB
then
co v und w in verschiedenen Bäumen oc
MSB:=MSB 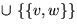 ; if
; if 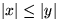 then
co Baum x enthält
then
co Baum x enthält 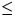 Knoten als Baum y oc
co y:= Union(x,y) oc
else
vereinige x und y, mit y neues Kind der Wurzel von x;
fi
fi
od
Knoten als Baum y oc
co y:= Union(x,y) oc
else
vereinige x und y, mit y neues Kind der Wurzel von x;
fi
fi
od
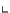
Korrektheit: Falls die Gewichte eindeutig sind (w() injektiv), folgt
die Korrektheit direkt aus der ``blauen`` und ``roten`` Regel. Ansonsten
Induktion über die Anzahl der Knoten (|V|):
Ind. Anfang: |V| klein: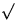
Sei 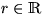 ,
, 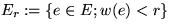 .
.
Es genügt zu zeigen:
Sei 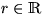 , sei
, sei 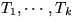 ein minimaler Spannwald (d.h. Spannwald minimalen
Gewichtes) für
ein minimaler Spannwald (d.h. Spannwald minimalen
Gewichtes) für 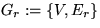 (d.h.betrachte nur Kanten mit Gewicht >r). Sei T
ein MSB von G, dann:
(d.h.betrachte nur Kanten mit Gewicht >r). Sei T
ein MSB von G, dann:
Hilfsbehauptung: Die Knotenmenge eines jeden Ti im T induziert einen
zusammenhängenden Teilbaum.
Beweis der Hilfsbehauptung:
Sei Ti=:(Vi,Ei) und sei 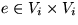 . Falls
. Falls 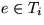 , dann ist nichts zu zeigen.
Für den Fall
, dann ist nichts zu zeigen.
Für den Fall 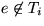 betrachte den Fundamentalkreis C, den e in Ti erzeugt.
Gewicht aller Kanten auf
betrachte den Fundamentalkreis C, den e in Ti erzeugt.
Gewicht aller Kanten auf 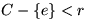 . Falls die beiden Endpunkte von e in T durch einen
Pfad verbunden sind, der eine Kante
. Falls die beiden Endpunkte von e in T durch einen
Pfad verbunden sind, der eine Kante 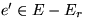 enthält, dann liefert die ``rote`` Regel,
daß T nicht minimal ist.
enthält, dann liefert die ``rote`` Regel,
daß T nicht minimal ist.
 Die beiden Endpunkte und e sind in T durch einem Pfad aus lauter Kanten
mit Gewicht <r verbunden.
Die beiden Endpunkte und e sind in T durch einem Pfad aus lauter Kanten
mit Gewicht <r verbunden.

Zeitkomplexität: (mit n=|V|, m=|E|)
| Sortieren |
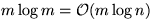 |
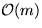 Find
-Operationen
Find
-Operationen |
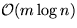 |
|---|
| n-1
Unions |
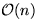 |
|---|
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:} Kruskal's MSB-Algorithmus hat die Zeitkomplexit\uml {a}t
von $\mathcal{O}((m+n)\log n)$
}}](img871.gif)
Beweis: s.o.

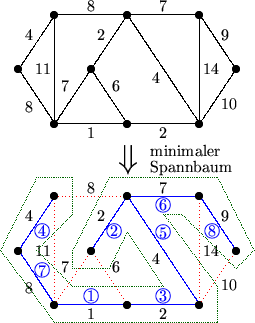
Beispiel für Kruskals Algorithmus:




Next: Prim's Algorithmus, erste Variante
Up: Grundlagen
Previous: Generischer minimaler Spannbaum-Algorithmus
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]() sortiere die Kanten nach aufsteigendem Gewicht in eine Liste L;
initialisiere
sortiere die Kanten nach aufsteigendem Gewicht in eine Liste L;
initialisiere ![]() Wald (n=|V|) mit
Wald (n=|V|) mit ![]() co G=(V,E),
co G=(V,E), ![]() oc
co implementiere Ti's als in-Trees mit den jeweiligen Wurzeln als
Repräsentanten; allgemein: Unio-Find-Problem oc
MSB:=
oc
co implementiere Ti's als in-Trees mit den jeweiligen Wurzeln als
Repräsentanten; allgemein: Unio-Find-Problem oc
MSB:=![]() ; for i:=1 to length(L) do
; for i:=1 to length(L) do
![]() ; x:= Baum
; x:= Baum ![]() , der v enthält; co x:= Find(v) oc
y:= Baum
, der v enthält; co x:= Find(v) oc
y:= Baum ![]() , der w enthält; co y:= Find(w) oc
if
, der w enthält; co y:= Find(w) oc
if ![]() then
co v und w in verschiedenen Bäumen oc
MSB:=MSB
then
co v und w in verschiedenen Bäumen oc
MSB:=MSB ![]() ; if
; if ![]() then
co Baum x enthält
then
co Baum x enthält ![]() Knoten als Baum y oc
co y:= Union(x,y) oc
else
vereinige x und y, mit y neues Kind der Wurzel von x;
fi
fi
od
Knoten als Baum y oc
co y:= Union(x,y) oc
else
vereinige x und y, mit y neues Kind der Wurzel von x;
fi
fi
od
![]()