Next: Traversierung von Graphen
Previous: Minimale Spannbäume
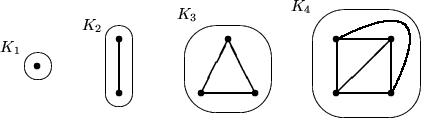
Ein Graph G=(V,E) besteht aus einer Menge von Knoten V und einer Menge Kanten
E. Die Anzahl der Knoten bezeichnen wir mit n (|V|=n), die Anzahl der Kanten
mit m (|E|=m). Eine Kante 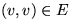 heißt
Schlinge
. Falls E eine Multimenge
ist, spricht man von
Mehrfachkanten
. Kanten (u,v) und (v,u) heißen
antiparallel
.
Graphen ohne Schlingen und Mehrfachkanten
bezeichnen wir mit
einfachen Graphen
(eng. simple). Formal definiert:
heißt
Schlinge
. Falls E eine Multimenge
ist, spricht man von
Mehrfachkanten
. Kanten (u,v) und (v,u) heißen
antiparallel
.
Graphen ohne Schlingen und Mehrfachkanten
bezeichnen wir mit
einfachen Graphen
(eng. simple). Formal definiert:
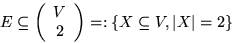
In diesem Fall bezeichnet man G=(V,E) als einen
ungerichteten Graphen.
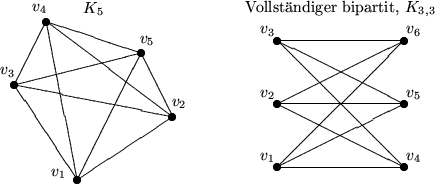
Graphische Darstellung:
Ist 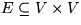 , dann heißt G
gerichteter Graph
, für
, dann heißt G
gerichteter Graph
, für 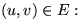

Der zu G gehörige ungerichtete Graph ist G'=(V,E'). E' erhält man, indem man in E
die Richtungen wegläßt und Mehrfachkanten beseitigt.
Sei 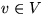 , unter der
Nachbarschaft
, unter der
Nachbarschaft
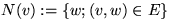 eines Knotens v versteht
man die Menge der direkten Nachbarn von v. Der
Grad
eines Knotens ist definiert als:
eines Knotens v versteht
man die Menge der direkten Nachbarn von v. Der
Grad
eines Knotens ist definiert als:
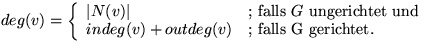
Dabei sind indeg(v) die Anzahl aller Kanten, die v als Endknoten haben, und outdeg(v)
die Anzahl aller Kanten, die v als Startknoten haben.

![\fbox {\parbox[c]{12.45cm}{\textbf{Korollar:}
In jedem Graphen ist die Anzahl der Knoten mit ungeradem Grad eine gerade Zahl.
}}](img790.gif)
Das
Komplement
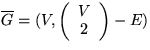 eines
Graphen G=(V,E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des
vollständigen Graphen ohne die Kantenmenge E.
eines
Graphen G=(V,E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des
vollständigen Graphen ohne die Kantenmenge E.
Ein Graph H=(V',E') heißt
Teilgraph
(aka. Subgraph, Untergraph, ...)
von G=(V,E), falls 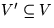 und
und 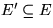 . H heißt
(knoten-) induzierter
Teilgraph,
falls H Teilgraph von G ist, und es gilt
. H heißt
(knoten-) induzierter
Teilgraph,
falls H Teilgraph von G ist, und es gilt 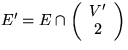 .
.
Ein
Kantenzug
ist eine Folge 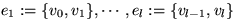 , wobei alle
ei verschieden sind. v0 und vl bezeichnen wir als Endknoten. Die Länge des Kantenzuges
bezeichnen wir mit l. Sind bei einem Kantenzug auch alle vi verschieden, so sprechen wir von
einem
Pfad.
Ein Kantenzug mit vl=v0 heißt
Zykel
. Ein Zykel, in dem alle vi
verschieden sind, heißt
Kreis
.
, wobei alle
ei verschieden sind. v0 und vl bezeichnen wir als Endknoten. Die Länge des Kantenzuges
bezeichnen wir mit l. Sind bei einem Kantenzug auch alle vi verschieden, so sprechen wir von
einem
Pfad.
Ein Kantenzug mit vl=v0 heißt
Zykel
. Ein Zykel, in dem alle vi
verschieden sind, heißt
Kreis
.
Ein Graph G heißt
zusammenhängend
, wenn es für alle
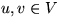 einen Pfad gibt, der u und v verbindet. Ein (kanten-) maximaler zusammenhängender
Teilgraph heißt
(Zusammenhangs-)Komponente
.
einen Pfad gibt, der u und v verbindet. Ein (kanten-) maximaler zusammenhängender
Teilgraph heißt
(Zusammenhangs-)Komponente
.
Ein Graph G ist
azyklisch
, wenn er keine
Kreise enthält. Wir bezeichnen diesen dann als
Wald
. Ist dieser auch zusammenhängend,
so sprechen wir von einem
Baum
. Ist der Teilgraph 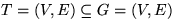 ein Baum,
dann heißt T ein
Spannbaum
.
ein Baum,
dann heißt T ein
Spannbaum
.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:} Ist $T=(V,E)$\space ein Baum, dann ist $\vert E\vert=\vert V\vert-1$.
}}](img799.gif)
Beweis: Induktion über die Anzahl der Knoten:
n=0,1 : klar.
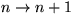 : Sei
: Sei 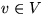 ,
, 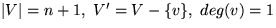 .
.
Solche Knoten müssen existieren, denn ansonsten würde ein Zykel entstehen, und das wäre ein
Widerspruch zur Definition eines Baumes.
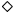
![\fbox {\parbox[c]{12.45cm}{\noindent\textbf{Korollar:} Ein Graph $G$\space ist zusammenh\uml {a}ngend, g.d.w.
$G$\space ein Spannbaum hat.
}}](img802.gif)
Minimale Spannbäume
![]()
![]() , dann heißt G
gerichteter Graph
, für
, dann heißt G
gerichteter Graph
, für ![]()
![]()
![]() , unter der
Nachbarschaft
, unter der
Nachbarschaft
![]() eines Knotens v versteht
man die Menge der direkten Nachbarn von v. Der
Grad
eines Knotens ist definiert als:
eines Knotens v versteht
man die Menge der direkten Nachbarn von v. Der
Grad
eines Knotens ist definiert als:
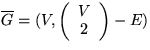 eines
Graphen G=(V,E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des
vollständigen Graphen ohne die Kantenmenge E.
eines
Graphen G=(V,E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des
vollständigen Graphen ohne die Kantenmenge E. 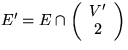 .
.