Prim's Algorithmus, zweite Variante

Idee: Lasse die Priority Queues nicht zu groß werden.
Sei $G=(V,E),\ \vert V\vert=n,\ \vert E\vert=m$, w Gewichtsfunktion, k Parameter, der unten festgelegt wird.
Der Algorithmus wird in den folgenden Phasen abgearbeitet:

1.

Initialisiere eine Schlange von Bäumen, jeder Baum anfangs (Super-) Knoten. Zu jedem Baum: Priority Queue (Fibonacci-Heap) mit den Nachbarn der Knoten im Baum, die selbst nicht im Baum sind. Schlüssel: Gewicht einer leichtesten Kante zu einem Knoten im Baum.

2.

Markiere jeden Baum in der Schlange mit der Nummer der laufenden Phase

3.

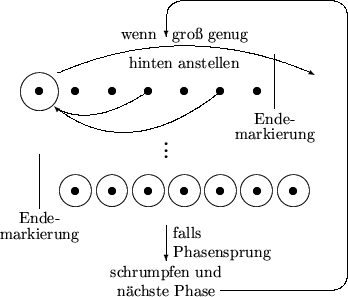
while vorderster Baum in der Schlange hat laufende Phasennummer do
		 lasse ihn wachsen, solange seine Priority Queue weniger als
		 k Elemente enthält (und noch was zu tun ist)
		if Priority Queue zu groß then
		 		 füge Baum mit Phasennummer + 1 am Ende der Schlange ein
		 fi
od    

4.

Falls ,,Phasensprung``: Schrumpfe alle Bäume zu Superknoten, reduziere Kantenmenge (Behalte zwischen zwei Knoten, jeweils nur die leichteste Kante).

5.

nächste Phase!

Betrachte Schlange von Bäumen:

(Arbeit pro Phase $\sim$ # Knoten, außer Vereinigung zweier Superknoten T₁ und T₂.)
Für jeden (Super-)Knoten v in T₂'s Priority Queue:

1.

$v \in T_1$: $\surd$ (nichts zu tun)

2.

v in Priority Queue von T₁, einfügen bzw. conditional DecreaseKey . Hilfsdatenstruktur: für alle Knoten in den Priority Queues ein Zeiger auf den Superknoten, in dessen Priority Queue der Knoten letztmals am Anfang der Schlange stand.

3.

sonst: Einfügen

Betrachte Knoten mit ,,Halbkanten``: jede Halbkante kommt nur 1x in den Bäumen vor. Mit m Kanten ergeben sich 2m Halbkanten, d.h. Anzahl proportional zu m.

Zeitaufwand pro Phase: (+ Superknoten zu Beginn)

• Initialisierung: $\mathcal{O}(m)$
• Delete und DeleteMin : $\leq t$
• sonstige Priority Queue-Operationen, Overhead: $\mathcal{O}(m)$

Da die Priority Queues höchstens k Elemente enthalten, wenn darauf eine Priority Queue-Operation durchgeführt wird, sind die Kosten pro Phase

$$\mathcal{O}(t \log k + m)$$

Setze $k=2^{\frac{2m}{t}}$ (damit $t \log k = m$). Damit sind die Kosten pro Phase $\mathcal{O}(m)$.

Wieviele Phasen? Sei t die Anzahl der Superknoten am Anfang einer Phase, t' diese Zahl zu Beginn der nächsten Phase. Sei a die durchschnittliche Anzahl ursprünglicher Knoten in den t Priority Queues zu Anfang der Phase, a' entsprechend zu Beginn der nächsten Phase.

Wir haben:

1.

$a = \frac{2m}{t}$

2.

$t' \leq \frac{2m}{k}$ (mit Ausnahme ev. der letzten Phase)

Also:

$$a' = \frac{2m}{t'} \geq k = 2^{\frac{2m}{t}} = 2^a$$

Für die erste Phase ist $a=\frac{2m}{n}$, a ist für jede Phase $\leq n-1$. Also ist die Anzahl der Phasen

$$\leq 1 + \min \left\{ i; \log_2^{(i)}(n-1) \leq \frac{2m}{n} \right\}$$

Setzen wir $\beta(m,n) := \min \left\{ i; \log_2^{(i)}n \leq \frac{m}{n} \right\}$, dann gilt

$$\beta(m,n) \leq \log^* n \text{ f\uml {u}r } n \leq m \leq \binom{n}{2}$$

Euklidische minimale Spannbäume stellen ein Problem dar, für das es speziellere Algorithmen gibt. Literatur hierzu:
A.C.-C. Yao: Constructing Minimum Spanning Trees in k-dimensional spaces and related problems. SIAM Journal on Computing $\underline{11}$(4) p. 721-736 (1982).