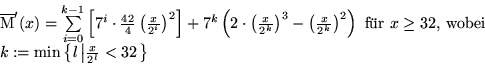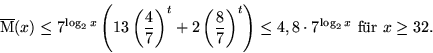![]()
Bilde:
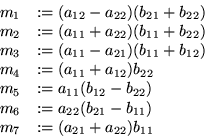
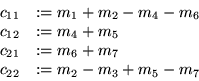
![]()
![]()
kill
co A und B sind
Matrizen oc if n<16 then berechne
mit klassischer Methode else if n gerade then spalte A und B in je 4
Matrizen auf und wende Strassen's Formeln an. Führe die Multiplikationen rekursiv mit Matmult aus. else spalte A und B in je eine
Matrix (A11,B11) und drei verbleibende Blöcke auf. Wende Matmult rekursiv auf A11, B11 an und berechne die anderen Produkte mit klassischer Methode. fi fi
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Der Matmult-Algorithmus hat folgende E...
...e mehr als $4.8n^{\log_2 7}$\space arithmetische
Operationen.\end{enumerate}}}](img1189.gif)
Beweis:
![]()
![]()
![]()
![]()