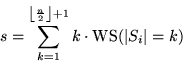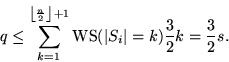Next: Matrizenmultiplikation à la Strassen
Up: Kürzeste Pfade
Previous: Ein besserer Algorithmus für
Ein Algorithmus für die transitive Hülle mit lin. erwarteter Laufzeit
Ein Algorithmus für die transitive Hülle in Digraphen mit linearer erwarteter Laufzeit
Die Wahrscheinlichkeit eines Digraphen mit n Knoten und m Kanten ist (nur) eine Funktion von n und m.
Daraus folgt (wir lassen der Einfachheit halber Schleifen (=Kanten 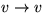 ) zu), daß jede Kante
(u,v) mit Wahrscheinlichkeit
) zu), daß jede Kante
(u,v) mit Wahrscheinlichkeit 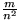 vorhanden ist, falls wir Graphen mit n Knoten und m
Kanten betrachten.
vorhanden ist, falls wir Graphen mit n Knoten und m
Kanten betrachten.
Einschub: Breitensuche (BFS): Schlange, queue, FIFO:
Durchlaufe Graphen, indem wir, solange möglich den vordersten Knoten v aus der Queue nehmen,
ihn behandeln und die Liste seiner noch nicht behandelten Nachbarn in die queue hinten
einfügen.
Beispiel:
algorithm exp-lin-transitive-closure
(C.P. Schnorr, An Algorithm for Transitive Closure with Linear Expected Time, SIAM Journal
on Computing 7 (1978), pages 127-133.)
Phasen:
- 0.
- Konstruiere die linear geordneten Adjazenzlisten
 des
Graphen Gr (entsteht aus G durch Umkehrung aller Knoten).
des
Graphen Gr (entsteht aus G durch Umkehrung aller Knoten).
Beispiel:
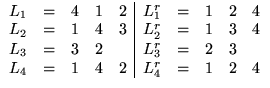
Ersetze ebenfalls alle Li durch Lrri (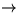 sortierte Adjazenzlisten)
sortierte Adjazenzlisten)
- 1.
- Berechne für jeden Knoten i in BFS-Art eine Liste Si von von i aus
erreichbaren Knoten, so daß (i) oder (ii) gilt:
- (i)
 und Si enthält alle von
i aus erreichbaren Knoten
und Si enthält alle von
i aus erreichbaren Knoten
- (ii)
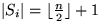
- 2.
- Entsprechende Listen Pi von Vorgängern von i
- 3.
-
for i:=1 to n do
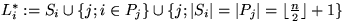 ;od
;od
Bilde (L*i)rr für 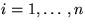
Korrektheit: 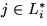 g.d.w. (i,j) in transitiver Hülle.
g.d.w. (i,j) in transitiver Hülle.
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei die Wahrscheinlichkeit eines Graph...
...wert f\uml {u}r die Anzahl der Kanten in
der transitiven H\uml {u}lle ist.
}}](img1146.gif)
Beweis:
Das Durchlaufen des Graphen (von V1 aus für die Konstruktion von
S1) in BFS-Manier liefert eine Folge 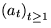 von Knoten.
Sei
von Knoten.
Sei 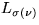 die
die 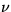 -te Adjazenzliste, die in der BFS erkundet
wird,
-te Adjazenzliste, die in der BFS erkundet
wird,
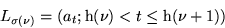
Sei 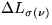 die Menge der at in
die Menge der at in 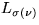 , und sei
, und sei
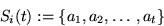
Wie bereits gezeigt, ist

Alle n-Tupel von geordneten Listen L1,L2,...,Ln mit
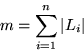
sind aufgrund der Voraussetzungen über die Wahrscheinlichkeitsverteilung
gleich wahrscheinlich.
Also:
Beobachtung 1: Die Mengen  sind
(paarweise) unabhängig.
sind
(paarweise) unabhängig.
Beobachtung 2: Die 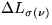 sind gleichverteilt, d.h. für
alle
sind gleichverteilt, d.h. für
alle 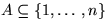 gilt:
gilt:

Lemma: Sei 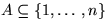 mit |A|=k. Sei
mit |A|=k. Sei
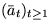 eine Folge von unabhängigen gleichverteilten
Zufallsvariablen mit Wertemenge
eine Folge von unabhängigen gleichverteilten
Zufallsvariablen mit Wertemenge 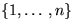 . Dann gilt:
. Dann gilt:
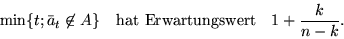
Beweis:
WS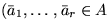 und
und
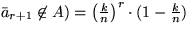 .
.
Also ist der Erwartungswert für min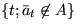 :
:
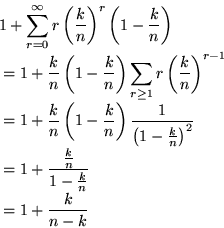

Anmerkung:
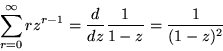
Lemma: Sei 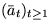 wie oben,
wie oben,  . Dann hat
min
. Dann hat
min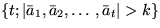 Erwartungswert
Erwartungswert
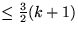 .
.
Beweis:
Wegen der Additivität des Erwartungswertes gilt: Der gesuchte Erwartungswert ist
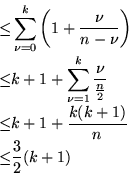

Wenn wir jedes 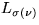 in sich zufällig permutieren, erhalten wir eine
Folge
in sich zufällig permutieren, erhalten wir eine
Folge 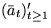 von Zufallsvariablen, so daß
von Zufallsvariablen, so daß
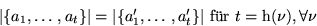
Da die at' innerhalb eines jeden Intervalls
h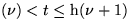 paarweise verschieden sind, gilt
für sie die vorhergehende Abschätzung erst recht. Daher sind
paarweise verschieden sind, gilt
für sie die vorhergehende Abschätzung erst recht. Daher sind
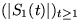 und
und 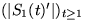 gleichverteilte Folgen von
Zufallsvariablen, denn dies gilt zunächst für alle Zeitpunkte der Form
gleichverteilte Folgen von
Zufallsvariablen, denn dies gilt zunächst für alle Zeitpunkte der Form
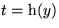 ; da aber für diese Zeitpunkte S1(t) = S1'(t) ist, und
; da aber für diese Zeitpunkte S1(t) = S1'(t) ist, und
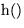 zufällig verteilt ist, ist auch die Verteilung der beiden Folgen
zwischen diesen Intervallgrenzen identisch.
zufällig verteilt ist, ist auch die Verteilung der beiden Folgen
zwischen diesen Intervallgrenzen identisch.
Sei s der Erwartungswert und sei |Si| die tatsächliche Größe von Si
nach der Phase 1. Dann
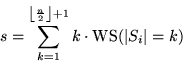
Die erwartete Anzahl der Schritte (und damit die Kosten) in der BFS sei q.
Dann gilt:
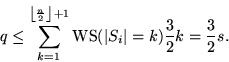
Also ist der Aufwand des Algorithmus für die Phasen 1 und 2 im Erwartungswert
 . Da ns=m*, und da die Kosten der anderen Phasen offensichtlich
durch
. Da ns=m*, und da die Kosten der anderen Phasen offensichtlich
durch 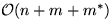 beschränkt sind, folgt die Behauptung.
beschränkt sind, folgt die Behauptung.





Next: Matrizenmultiplikation à la Strassen
Up: Kürzeste Pfade
Previous: Ein besserer Algorithmus für
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999
![]()
![]()
![\begin{picture}
(127,40)
\color {blue}
\multiput(35,35)(-2.5,0){4}{\bezier{...
...7.5){\makebox(27,12)[lt]{\underline{Bezeichnungen:}}}
% \end{small}\end{picture}](img1138.gif)

;od
![\fbox {\parbox[c]{12.45cm}{\textbf{Satz:}
Sei die Wahrscheinlichkeit eines Graph...
...wert f\uml {u}r die Anzahl der Kanten in
der transitiven H\uml {u}lle ist.
}}](img1146.gif)
![]()
![]()
![]()
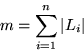
![]()
![]()
![]() und
und
![]() .
.
![]() :
:
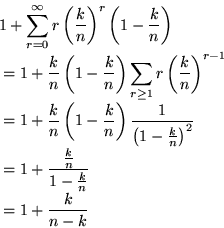
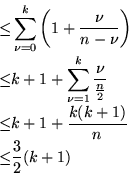
![]()