![]() co Sei
co Sei ![]() mit
mit 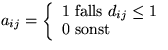 oc
co Sei B die Boolsche Einheitsmatrix oc
for l:=2 to r+1 do
oc
co Sei B die Boolsche Einheitsmatrix oc
for l:=2 to r+1 do
![]() for
for ![]() do
if bij=1 then dij(l):=l else
do
if bij=1 then dij(l):=l else ![]() fi;
if
fi;
if ![]() then dij(l):=dij(l-1) fi
od
od
then dij(l):=dij(l-1) fi
od
od
![]()

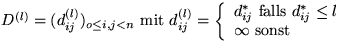
co Sei
mit
oc co Sei B die Boolsche Einheitsmatrix oc for l:=2 to r+1 do
for
do if bij=1 then dij(l):=l else
fi; if
then dij(l):=dij(l-1) fi od od
Dieser Algorithmus berechnet ![]() .
.
Sei ![]() eine Zahl
eine Zahl ![]() , so daß die Matrixmultiplikation in der Zeit
, so daß die Matrixmultiplikation in der Zeit
![]() durchgeführt werden kann (Winograd/Coppersmith:
durchgeführt werden kann (Winograd/Coppersmith: ![]() ).
).
Zeitaufwand für Algorithmus 1: ![]()
algorithm apsd =
apsd berechnet:
![]() Berechne, mit Algorithmus 1,
Berechne, mit Algorithmus 1, ![]() ;
l:=r;
for s:=1 to
;
l:=r;
for s:=1 to ![]() do
for i:=0 to n-1 do
finde in der i-ten Zeile von D(l) den Wert d,
do
for i:=0 to n-1 do
finde in der i-ten Zeile von D(l) den Wert d, ![]() , so daß d in der
i-ten Zeile am wenigsten oft vorkommt;
Si:= Menge der Spaltenindizes, in denen dieses d in der i-ten Zeile von
D(l) vorkommt;
od
, so daß d in der
i-ten Zeile am wenigsten oft vorkommt;
Si:= Menge der Spaltenindizes, in denen dieses d in der i-ten Zeile von
D(l) vorkommt;
od
![]() ; for
; for ![]() do
if
do
if ![]() then
then ![]() else
else ![]() fi;
if
fi;
if ![]() then dij(l1):=dij(l)
elseif
then dij(l1):=dij(l)
elseif ![]() then dij(l1)=mij
else
then dij(l1)=mij
else ![]() fi
od
l := l1;
od
fi
od
l := l1;
od
![]()
Zunächst ![]() , dann D(l) für
, dann D(l) für
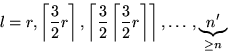
![]()
![]()
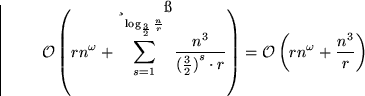

![]()