next up previous contents
Next: Ein besserer Algorithmus für Up: Transitive Hülle Previous: Der 4-Russen-Algorithmus für Boolesche

Transitive Hülle und DFS

Tiefensuche(DFS):

proc DFS-visit(node v) = 



$\ulcorner$markiere v;
num[v]:= ++count;
for alle Nachbarn u von v do
		 if u unmarkiert then DFS-visit(u)  fi
od
$\llcorner$
algorithm DFS = 



$\ulcorner$for alle Knoten v do unmarkiere(v);  num(v):=0 od;
count:=0;
for alle Knoten v do
		 if v unmarkiert then DFS-visit(v)  fi
od
$\llcorner$
Bemerkung: Funktioniert für Graphen und Digraphen.

Nachbarn in Graphen und Digraphen:


\begin{picture} (85,13) \multiput(10,10)(20,0){2}{\circle*{1}} \put(10,10){\li... ....5,11){\makebox(5,5)[b]{$v$}} \put(77.5,11){\makebox(5,5)[b]{$u$}}\end{picture}


Beispiele für DFS:

Graph G1:


\begin{picture} (114,40) \put(10,5){\circle*{1}} \put(0.5,15){\circle*{1}} \... ...(87.5,0){\makebox(5,4)[t]{10}} \put(107.5,0){\makebox(5,4)[t]{11}}\end{picture}

Digraph G2:


\begin{picture} (114,40) \put(10,5){\circle*{1}} \put(0.5,15){\circle*{1}} \p... ...t(87.5,0){\makebox(5,4)[t]{9}} \put(107.5,0){\makebox(5,4)[t]{10}}\end{picture}

  


\begin{picture} (60,35) \color {red} % Rueckwaertskanten \bezier{14}(0,15)(7... ...k} \put(0,22.5){\makebox(27,12)[lt]{\underline{Bezeichnungen:}}}\end{picture}

Bemerkung: Alle Baumkanten zusammen ergeben den DFS-Wald (Spannwald).


\begin{picture} (108,85) \put(15,10){\circle*{1}} \put(30,5){\circle*{1}} \p... ...makebox(10,5)[l]{SZK$_5$}} \put(95,45){\makebox(10,5)[l]{SZK$_6$}}\end{picture}

Bemerkung: SZK: starke Zusammenhangskomponente (in Digraphen)

DFS in ungerichteten zyklischen Graphen, n Knoten, m Kanten, n-1 Baumkanten, m-n+1 Rückwärtskanten.

Zeitaufwand: 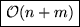\fbox {$\mathcal{O}(n+m)$}


\begin{picture} (55,40) \put(0,9){\makebox(10,5)[r]{SZK$_2$}} \put(12.5,9){\li... ...kebox(5,16){}}\right)$}} \put(5,32){\makebox(5,5){$\mathbf{A^*}$}}\end{picture}

A* aus DFS mit Aufwand 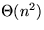$\Theta(n^2)$ in ungerichteten Graphen (Anm.: SZK = ZK).

DFS in gerichteten Graphen (Digraphen), n Knoten, m Kanten, Baum-, Vorwärts-, Rückwärts- und Querkanten:


\begin{picture} (95,30) \color [rgb]{0,0.6,0} \put(25,25){\vector(-1,-1){9.... ...2.5){\makebox(27,12)[lt]{\underline{Bezeichnungen:}}} % \end{small}\end{picture}

Zeitaufwand: 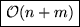\fbox {$\mathcal{O}(n+m)$}

Es gilt: u ist von v aus auf einem gerichteten Pfad erreichbar g.d.w. u Knoten in dem DFS-Baum (DFS-visit(v)) mit Wurzel v ist.
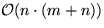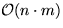Also: Transitive Hülle in Zeit $\mathcal{O}(n\cdot (m+n))$ bzw. $\mathcal{O}(n\cdot m)$. Sehr gut für dünne Graphen (also solche mit relativ wenigen Kanten).
next up previous contents
Next: Ein besserer Algorithmus für Up: Transitive Hülle Previous: Der 4-Russen-Algorithmus für Boolesche
Abbas-Bardia Kabiri-Jarghouyeh
3/3/1999